Plentiful perturbations

1. Intro
2. Taylor/Maclaurin expansions
3. Asymptotic series/expansions
4. Regular perturbations
5. Singular perturbations
6. Footnotes

Intro

My previous post employed a straightforward example to illustrate how adopting an “optimal” rescaling can unveil the underlying structure of certain perturbation problems. The method used was not limited to the particular example discussed therein; it is in fact one of the general strategies applicable across numerous perturbation scenarios. The present post is a follow-up discussion, in which I am planning to amplify some of the earlier ideas. I will focus briefly on the difference between regular and singular perturbation problems via a couple of elementary examples involving quadratic equations. The same ideas can be applied to equations involving polynomials of higher degrees (but the algebra is likely to get more tedious).

Taylor/Maclaurin expansions

Let’s start with a reminder of a basic theorem from Calculus. Broadly speaking, this result informs us that if we have a function whose first $(n+1)$ derivatives exist at the origin (for some $n\geq{1}$), then the values of the function near that particular location can be approximated by a polynomial of order $n$ together with some extra bit (a remainder).

Before we can state this result more precisely, some new notation is needed; more specifically, for any given differentiable function $f(x)$, we set

\[f^{(1)}(0)\equiv \dfrac{df}{dx}(0),\quad f^{(2)}(0)\equiv\dfrac{d^2f}{dx^2}(0),\quad\dots,\quad f^{(n)}(0)\equiv\dfrac{d^nf}{dx^n}(0),\dots .\]

The result anticipated above can now be stated more rigorously:

Taylor’s Theorem (at the origin): Suppose that the function $f=f(x)$ has $(n+1)$ continuous derivatives on an open interval $I$ containing the point $x=0$. The, for each $x\in I$,

\[f(x)= f(0)+ f^{(1)}(0)x+\dfrac{1}{2!}f^{(2)}(0)x^2+\dots + \dfrac{1}{n!}f^{(n)}(0)x^n+ \delta_{n+1}(x),\]

where

\[\delta_{n+1}(x)\equiv \dfrac{1}{n!}\int_0^x f^{(n+1)}(t)(x-t)^n dt.\]

The remainder term ($\delta_{n+1}$) above can also be expressed in the form given by Lagrange (in 1797)

\[\delta_{n+1} = \dfrac{1}{(n+1)!}f^{(n+1)}(c)x^{n+1},\quad \mbox{for some c between 0 and x}.\]

This immediately allows us to establish the upper bound

\[| \delta_{n+1}(x) |\leq \dfrac{K x^{n+1}}{(n+1)!},\]

where

\[K\equiv\max_{0\leq t\leq x}|f^{(n+1)}(t)|.\]

If $f$ is infinitely differentiable on $I$, then

\[f(x) = \sum_{k=0}^n\dfrac{1}{k!}f^{(k)}(0)x^k+\delta_{n+1}(x)\,\quad x\in I,\]

for all positive integers $n$. If for such infinitely differentiable function $\delta_{n+1}(x)\to{0}$ as $n\to\infty$ for each each $x\in I$, then

\[\sum_{k=0}^n\dfrac{1}{k!}f^{(k)}(0)x^k\to f(x),\quad\mbox{as }n\to\infty,\]

which is the same as

\[f(x) = \sum_{k=0}^\infty\dfrac{1}{k!}f^{(k)}(0)x^k. \tag{1}\]

In this case we say that $f(x)$ can be expanded as a Taylor series in $x$ at the origin. The name Maclaurin is often attached to such series (although Taylor considered them some twenty years before Maclaurin). Since we only need series expansions near the origin, we will refer to (1) as a Maclaurin series.

A lot of things can go wrong with this result, and its validity hinges upon several conditions being met. For example, if the sequence of numbers $f^{(n)}(0)$ ($n\geq{1}$) grows too quickly, it is possible that the right-hand side of (1) converges nowhere. This would be the case of a function for which $f^{(n)}(0) = (n!)^2$ for all $n\geq{1}$. As can be easily confirmed by the ratio test, the series

\[\sum_{k=0}^{\infty} n! x^n\]

has a radius of convergence equal to $0$, so for such functions (1) is meaningless.

It can also happen that a function may be defined on $I\equiv (-\alpha,\alpha)$, with $\alpha>0$, and have a Maclaurin series which converges on $I$ without the two being equal on $I$. A classic example is the function

\[f(x) =\begin{cases} 0\quad &\mbox{if}\quad x=0,\\ {}\quad &{}\\ {\mathrm{e}}^{-1/x^2}\quad &\mbox{if}\quad x\neq{0}; \end{cases}\]

in this case, the function is defined and its Maclaurin series converges on $\mathbb{R}$ but the two are not equal except at $0$.

There are several take-away points from this brief discussion:

1. trying to approximate an unknown function $f(x)$ by a polynomial in $x$, as in Taylor’s Theorem, can occasionaly be “risky”; it might or it might not work (this is very problem-dependent, so the outlook is still bright);
2. Taylor’s theorem (the expansion with the remainder) is applicable in general, and does not require the function to be infinitely differentiable.

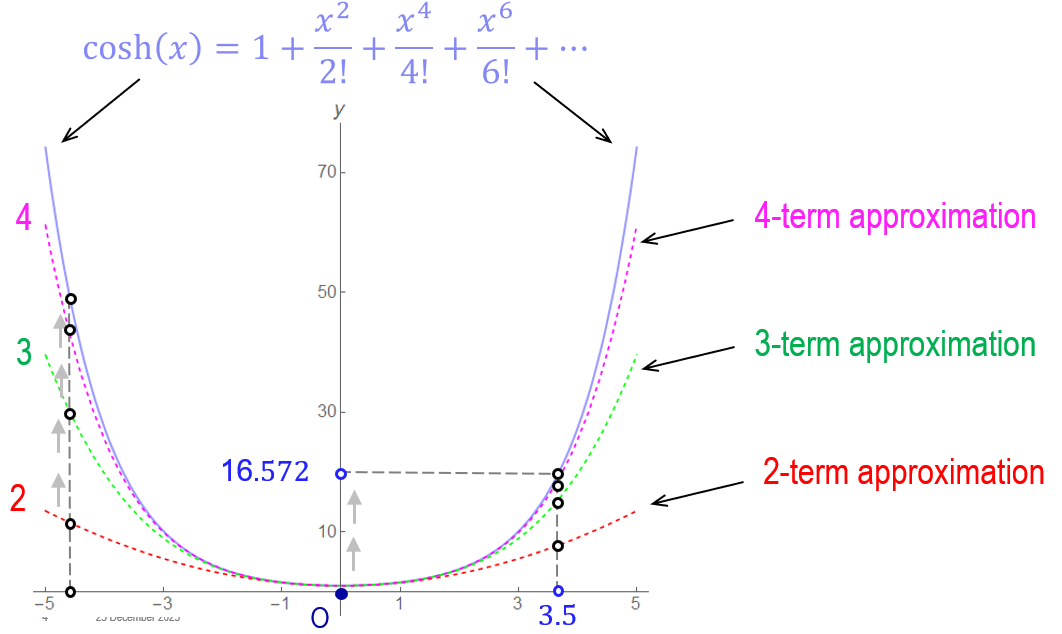
By way of example, let us look more closely to the Maclaurin expansion of a standard function, the usual hyperbolic cosine $f(x)\equiv\cosh(x)$; for $x$ close to $0$, Taylor’s Theorem gives

\[\cosh(x) = 1+\dfrac{x^2}{2!} + \dfrac{x^4}{4!} + \dfrac{x^6}{6!}+\dots. \tag{2}\]

When $x$ is fixed at a specific value ($x=a$, say), the right-hand side of (2) can be thought of as an estimate for the value $f(a)\equiv\cosh(a)$ if we keep only a finite number of terms on the right-hand side in

\[\cosh(a) = 1+\dfrac{a^2}{2!} + \dfrac{a^4}{4!} + \dfrac{a^6}{6!}+\dots.\]

The sum gets arbitrarily close to $\cosh(a)$ as we increase the number of terms on the right-hand side because the corresponding series is convergent. A visual illustration of this convergence is included below; the graph of the $\cosh$ function is compared against three different approximations obtained by suitably truncating the right-hand side in (2). Near the origin, all three approximate expressions seem acceptable, but the accuracy of the two-term approximation deteriorates rapidly as we move away from that point (e.g., $a\simeq{3.5}$).

Asymptotic series/expansions

Asymptotic expansions share several common features with the Macalurin series reviewed in the previous section, although there are two key differences: the former are not required to be convergent; also, more often than not asymptotic expansions involve negative and fractional powers. Our immediate goal is to describe the nature of an asymptotic series (albeit a particular class of these mathematical objects) by using an elementary example; we choose the function $\sin(x)$, which admits the convergent Maclaurin series

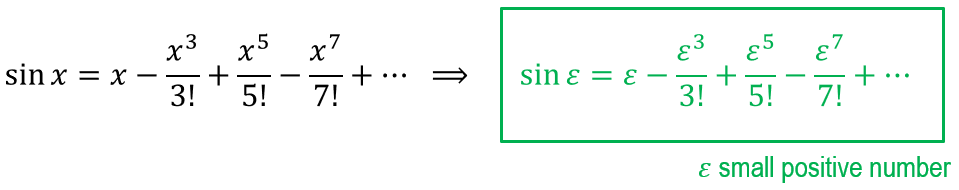
$x$ has been replaced by $\varepsilon$, a small positive number (something we normally indicate by writing $0<\varepsilon\ll{1}$).

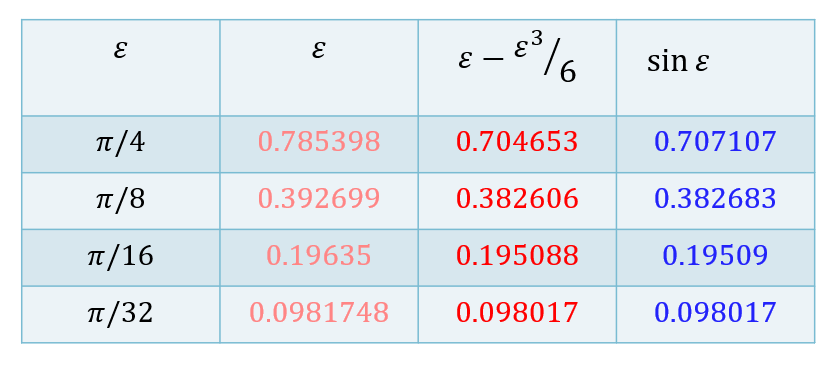
If we stop after the first term on the right-hand side (see green box above), there is an error $R_1$,

\[\begin{aligned}[t] &\sin\varepsilon = \varepsilon +R_1,\\ &{}\\ &R_1\equiv - \left(\dfrac{\varepsilon^3}{3!}+\dfrac{\varepsilon^5}{5!}-\dfrac{\varepsilon^7}{7!}+\dots\right). \end{aligned} \tag{3}\]

This error term is small, in the sense that $R_1/\varepsilon\to{0}$ as $\varepsilon\to{0}$, which is written as

\[R_1\ll\varepsilon,\quad\mbox{as }\varepsilon\to{0}.\]

Formula (3) represents a leading-order asymptotic approximation. We write that result as $\sin\varepsilon\sim\varepsilon$, and read it as: “ $\sin\varepsilon$ is asymptotically equal to $\varepsilon$ as $\varepsilon$ gets small”.

Note that the formula in the green box above also allows us to write

\[\begin{aligned}[t] &\sin\varepsilon =\left(\varepsilon-\dfrac{\varepsilon^3}{3!}\right)+R_3\\ &{}\\ &R_3\equiv \left(\dfrac{\varepsilon^5}{5!}-\dfrac{\varepsilon^7}{7!}+\dots\right). \end{aligned} \tag{4}\]

The new error term, $R_3$, satisfies $R_3/\varepsilon^3\to{0}$ as $\varepsilon\to{0}$; we write this as

\[R_3\ll\varepsilon^3,\quad\mbox{as }\varepsilon\to{0},\]

i.e. the error term is negligible compared to $\varepsilon^3$. The first equation in (4) is said to provide a two-term asymptotic approximation for $\sin\varepsilon$.

One can add more terms to the approximations obtained so far. A three-term approximation for $\sin\varepsilon$ corresponds to

\[\begin{aligned}[t] &\sin\varepsilon =\left(\varepsilon-\dfrac{\varepsilon^3}{3!}+\dfrac{\varepsilon^5}{5!}\right)+R_5\\ &{}\\ &R_5\equiv -\dfrac{\varepsilon^7}{7!}+\dots. \end{aligned} \tag{4}\]

We note in passing that $R_5/\varepsilon^5\to{0}$ as $\varepsilon\to{0}$ or, in other words,

\[R_5\ll\varepsilon^5,\quad\mbox{as }\varepsilon\to{0},\]

and so on.

Based on the features present in this example, a particular type of an asymptotic expansion is an expression of the form

\[a_0 + a_1\varepsilon + a_2\varepsilon^2 + a_3\varepsilon^3+\dots \tag{5}\]

where $a_j\in\mathbb{R}$ (some of them can be zero). Regarded as a series, (5) is not necessarily convergent. It must be emphasised that asymptotic expansions are significantly more general than (5), in that they might contain negative or fractional powers of $\varepsilon$ (and even more general expressions of $\varepsilon$¹).

Here are some important points to remember:

1. Convergent series: get increased accuracy by taking more and more terms (for $\varepsilon$ fixed).
2. Asymptotic expansions: get increased accuracy by taking $\varepsilon\to{0}$ (with a fixed number of terms).
3. More often than not asymptotic expansions are not convergent; this does not affect their usefulness.
4. Maclaurin series are asymptotic expansions (but the converse is not true).

The accuracy of the one- and two-term asymptotic approximations for the sine-function discussed above is illustrated below:

As already mentioned, not all functions admit Maclaurin expansions. Those that possess such expansions are often called regular, while those that don’t are labelled singular.

We are going to look at two simple examples of perturbation problems that involve regular or/and singular functions.

Regular perturbations

Consider the following quadratic depending on a (very) small parameter $\varepsilon>0$,

\[x^2-2x+\varepsilon = 0.\]

The usual formula applied to this example gives the roots in the form

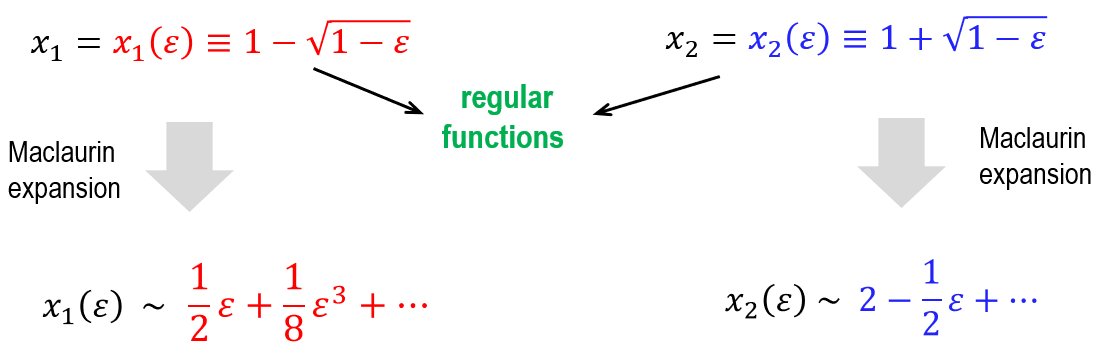
It is clear that both $x_1$ and $x_2$ are regular functions of $\varepsilon$ at the origin. Although in this case all the information follows immediately from the available closed-form expressions recorded above, we are interested in recovering the asymptotic expansions of the two roots by independent means. For a higher-order polynomial equation it is quite likely that an analytical expression for the roots won’t be available. To this end, we use the (unknown) Maclaurin expansions for the functions $x_j\equiv x_j(\varepsilon)$ for $j=1,2$, and aim to identify their coefficients by using implicit differentiation. This is explained next.

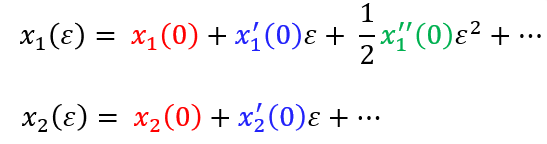
Start by setting $\varepsilon=0$ in the actual equation

\[x^2(\varepsilon)-2x(\varepsilon)+\varepsilon = 0\quad\Longrightarrow\quad x_1(0)=0,\quad x_2(0) = 2.\]

Next, differentiate with respect to $\varepsilon$

\[x^2(\varepsilon)-2x(\varepsilon)+\varepsilon = 0\quad\Longrightarrow\quad 2x(\varepsilon)x'(\varepsilon)-2x'(\varepsilon)+1 = 0, \tag{3}\]

whence

\[x'(\varepsilon) = \dfrac{1}{2-2x(\varepsilon)}\quad\Longrightarrow\quad x_1'(0)=\dfrac{1}{2},\quad x_2'(0) = -\dfrac{1}{2}.\]

Differentiating once again with respect to $\varepsilon$ the last relation in (3) yields

The process outlined above can be continued indefinitely.
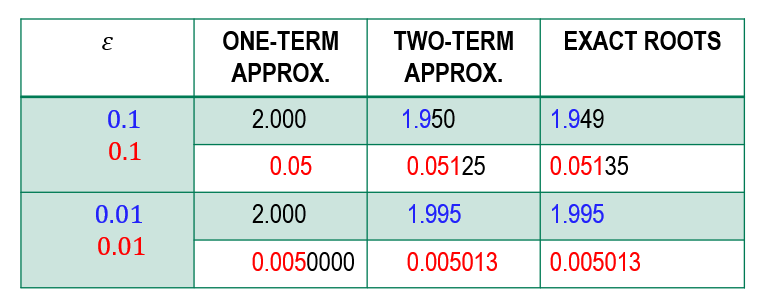
In conclusion, we have found (without solving the original quadratic) the following approximations

\[x_1 \simeq \dfrac{1}{2}\varepsilon + \dfrac{1}{8}\varepsilon^2\quad\mbox{and}\quad x_2\simeq 2-\dfrac{1}{2}\varepsilon.\]

The accuracy of these predictions is illustrated below for $\varepsilon=10^{-1}$ and $\varepsilon=10^{-2}$

Singular perturbations

Let’s change slightly the previous problem: instead of having $\varepsilon$ in the free term of our equation, we now move it next to the quadratic term (i.e. $x^2$). We take advantage of the closed-form solution to explore the nature of the roots; this information is included below:

Note that while one of the roots remains small as $\varepsilon$ gets progressively smaller, the other one blows up. The former can be approximated by following an identical strategy as in the previous section. However, the method fails to capture the second root because the function $x_2=x_2(\varepsilon)$ is not regular at $\varepsilon=0$. To circumvent this difficulty a change of tack is necessary; a suitable re-scaling turns out to do the trick.

We introduce the re-scaled variable $X\equiv \varepsilon{x}$ (or, equivalently, $x=X/\varepsilon$), and transform the original quadratic in terms of the new variable. This gives

\[X^2 -2X +\varepsilon = 0,\]

which is immediately recognised as being the equation we have already dealt with before. Once we have the approximations for the $X$-roots, we can then revert back to the $x$-variable to get

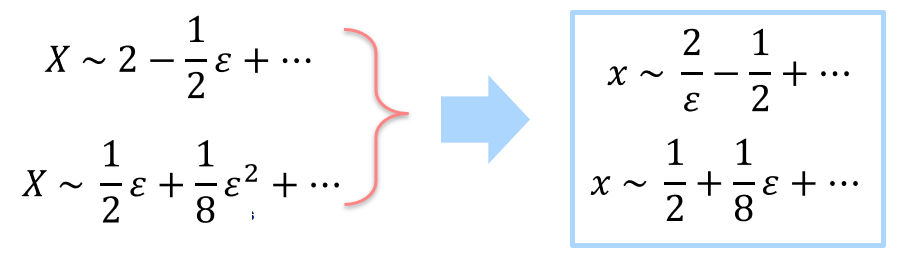
The first term in the approximation of the first root (blue box above) is the dominant one; clearly, that expression blows up as $\varepsilon\to{0}$.

Detailed discussion about asymptotic expansions can be found in any text¹, ², ³, ⁴ on perturbation/asymptotic methods. A short sample of some of the less demanding ones is included below.

Footnotes

1. Erdelyi, A.: Asymptotic Expansions. Dover Publications, Mineola NY (2003). ↩ ↩²

2. de Bruijin, N.G.: Asymptotic Methods in Analysis. Dover Publications, Mineola NY (2003). ↩

3. Paulsen, W.: Asymptotic Analysis and Perturbation Theory. CRC Press, Boca Raton (2014). ↩

4. Awrejcewicz, J., Krysko, V.A.: Introduction to Asymptotic Methods. Chapman & Hall/CRC, Boca Raton (2006) ↩