Schwarz and the Milkmaid

1. Intro
2. H.A. Schwarz
3. The Milkmaid puzzle
4. Back to the minimum perimeter
5. Final remarks
6. Footnotes

Intro

The subject of today’s post represents a noteworthy intersection of mathematical rigour and recreational puzzles. Among the protagonists in this narrative is the 19-th century German mathematician Hermann Amandus Schwarz (1843-1921), a significant presence in the annals of mathematics who taught at Gottingen University and later in Berlin. His legacy transcends rigorous mathematical investigations, touching upon engaging and accessible problems that contribute to the broader appeal of mathematical exploration.

Here is the main problem that I’ll be discussing:

Given a triangle $ABC$, consider $P$ between $B$ and $C$, $R$ between $A$ and $C$, $Q$ between $A$ and $B$. The points $P$, $Q$, $R$ are the vertices of a new triangle $PQR$, which is typically referred to as an inscribed triangle (in $\Delta{ABC}$); see the sketch included below. The question is to find such an inscribed triangle that has minimum perimeter.

In other words, we are asked to identify the locations of the points $P$, $Q$, $R$ on the corresponding sides of the given triangle $ABC$, such that

\[PQ + QR + RP\quad\mbox{is minimum}.\]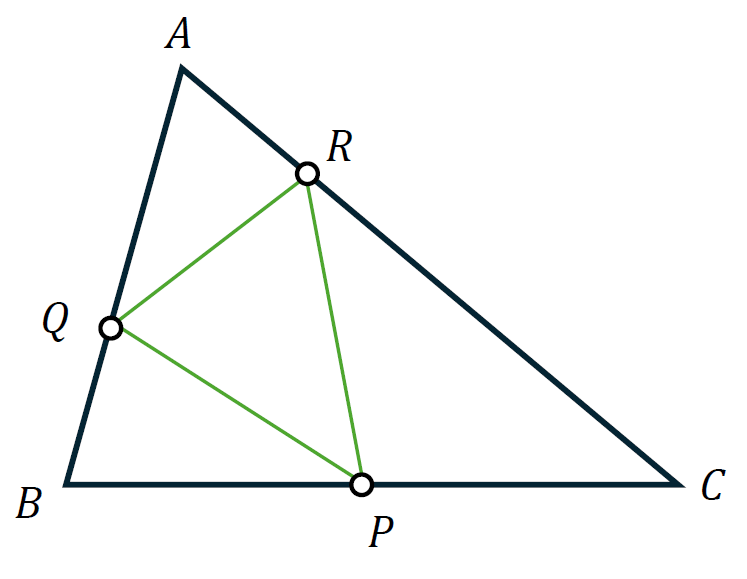

The above problem was originally posed and solved by Schwarz.

H.A. Schwarz

Schwarz was a notable German mathematician who is perhaps best remembered for his work on the so-called Schwarz-Christoffel Formula (SCF) related to conformal mappings. Once a popular topic in undergraduate electrical engineering programs¹, the SCF has experienced a decline in appeal and popularity over the last few decades. So much so, that the classic text of mathematical methods by Weber and Arfken² devotes only two pages to it and states:

…The method is often beautiful if there is a high degree of symmetry present but often impossible if the symmetry is broken or absent… Because of these limitations and primarily because high-speed electronic computers offer a useful alternative (….), the details and applications of conformal mappings are omitted.

In the theoretical developments of the SCF an important role is played by the following result (due to Schwarz as well)³⁴:

The Reflection Principle: Let $\Omega\neq\emptyset$ be a domain which is symmetric with respect to the real axis (i.e., for any $z\in\Omega$ its complex conjugate $\bar{z}$ is also in $\Omega$). Consider the subsets:

\[\begin{aligned} &\Omega_+:= \lbrace z\in\Omega:\quad \mbox{Im}(z)>0 \rbrace, \\ &{}\\ &\Omega_-:=\lbrace z\in\Omega:\quad \mbox{Im}(z)<0 \rbrace,\\ &{}\\ &\Omega_0:=\lbrace z\in\Omega:\quad \mbox{Im}(z)=0 \rbrace. \end{aligned}\]

A particular example of these subsets is included below:

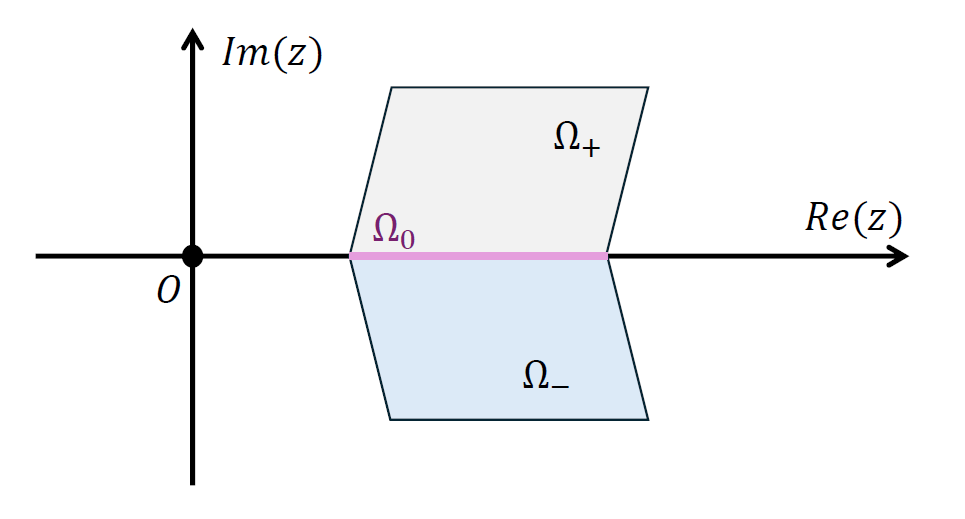
If $f$ is continous on $\Omega_+\cup\Omega_0$, analytic on $\Omega_+$, and $f(\Omega_0)\subset\mathbb{R}$, then the function $\widehat{f}:\Omega\to\mathbb{C}$ defined by

\[\widehat{f}(z) = \begin{cases} f(z)\quad\mbox{if }z\in\Omega_+\cup\Omega_0,\\ {}\\ \overline{f(\bar{z})}\quad\mbox{if }z\in\Omega_{-}. \end{cases}\]

is analytic. The function $\widehat{f}$ provides an analytic continuation of $f$ to the whole of the domain $\Omega$.

The actual statement of this important result is far more general. It deals with analytic functions in a domain that abuts on one side of an analytic curve (in the above formulation the curve is part of a straigh line – the real axis). It asserts that under certain conditions, the analytic function extends analytically across the curve and there is an explicit formula for this extension.

The proof of the simplified reflection principle given here is easily established by using the following auxiliary result:

Proposition: Let $f:\Omega\to\mathbb{C}$ be complex differentiable at $a\in\Omega$, and let

\[\Omega^{*} := \lbrace z\in\mathbb{C}: \bar{z}\in\Omega \rbrace .\]

Then the function $F:\Omega^{*}\to\mathbb{C}$ defined by $F(z) := \overline{f(\bar{z})}$ is complex differentiable at $z=\bar{a}$, and we have

\[F'(\bar{a})= \overline{f'(a)}.\]

The Milkmaid puzzle⁵

A lighter variant of the Schwarz minimum problem concerning the inscribed triangle is referred to as the “milkmaid problem.” This puzzle has gained recognition in the realm of popular mathematics literature for well over a century (the sketch included below is from Dudeney’s book, originally published in 1917 – see problem 187 therein).

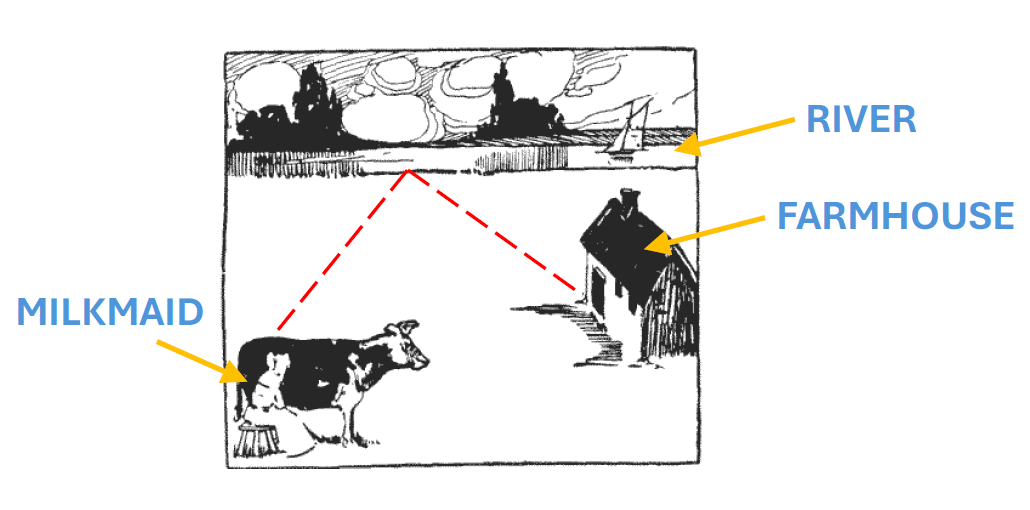
After she finishes her job with the cow, the milkmaid walks to the river before returning to the farmhouse (or the dairy). The question is⁵:

draw a line from the milking-stool down to the river and thence to the door of the dairy, which shall indicate the shortest possible route for the milkmaid. That is all. (…) Can you find that spot?

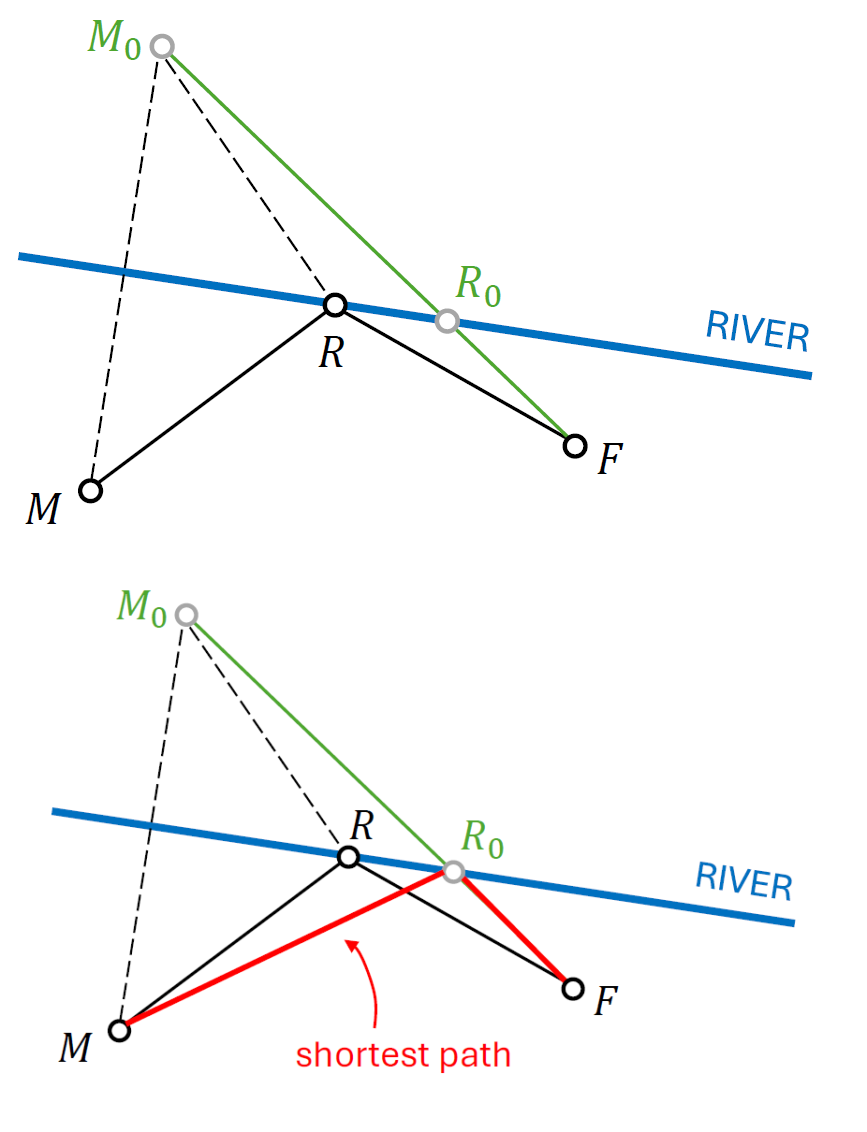
I am sure you can. But here’s the solution, just in case. A clear diagram always helps. Let $M$ indicate the position of the cow + milkmaid, and $F$ the location of the farmhouse. We are asked to identify the point $R$ on the blue line, such that $MR+RF$ is minimum. In the diagram included below I also considered two arbitrary points $R’$ and $R’’$ to indicate other possible routes. If $R$ is the solution of the milkmaid problem, then

\[MR+RF < MR' + R'F\quad\mbox{and}\quad MR+RF < MR''+R''F, \quad\mbox{etc.}\]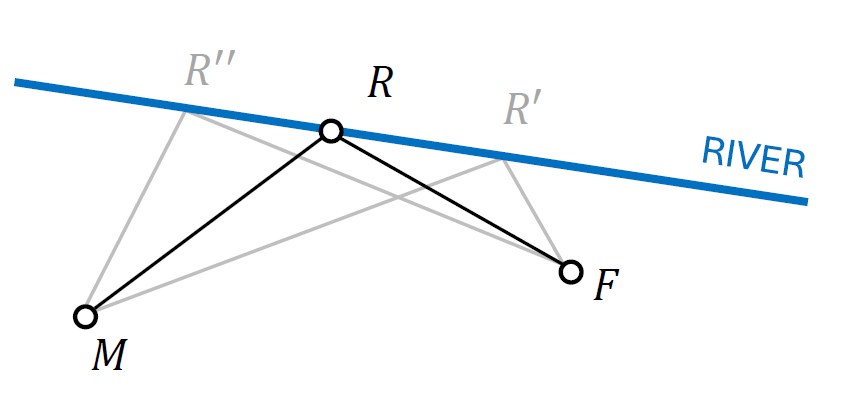

Differential calculus could help, but it is not really needed here. We start by considering $M_0$, the reflection of the point $M$ in the line that represents the river. This means that $MM_0$ is orthogonal to the blue line, and the perpendicular distances from $M$ and $M_0$ to this line are equal to each other. Clearly, for any $R$ on the blue line $MM_0R$ is an isosceles triangle, and hence $MR=M_0R$. The distance travelled by the milkmaid can then be equivalently expressed as $M_0R+RF$. But the shortest distance between two points ($M_0$ and $F$) on a plane is a straight line. So let’s join $M_0$ to $F$, and call $R_0$ the point where this new line intercepts the blue one. The solution to the milkmaid problem is the point $R_0$ because

\[MR+RF = M_0R + RF \geq M_0R_0 + R_0F = MR_0 + R_0F.\]

If $\theta_1$ represents the (acute) angle between $MR_0$ and the blue line, and $\theta_2$ the (acute) angle between $R_0F$ and the same line, then $\theta_1=\theta_2$. If we replace the river with a vertical mirror, the shortest path for the milkmaid would be the same as that of a ray of light starting at $M$ and reflected by the mirror back to the farmhouse.

Back to the minimum perimeter

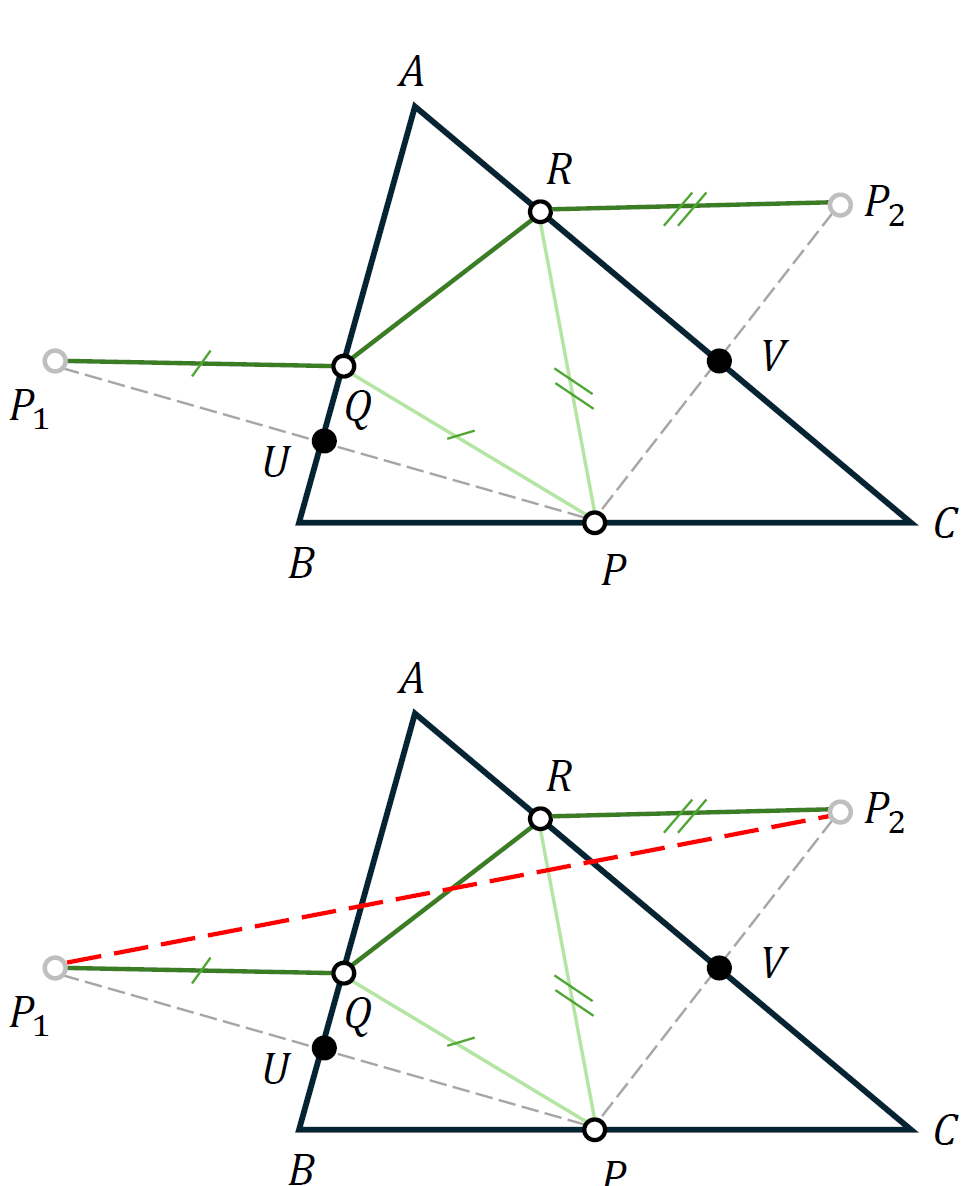
The solution of the original problem that appears at the beginning of this post is very similar to what we did above. Let’s start be reflecting $P$ (an arbitrary point between $B$ and $C$) in the lines $AB$ and $AC$. Using the first sketch below, $PP_1\perp AB$ and $PU = UP_1$; also, $PP_2\perp AC$ and $PV = VP_2$. Note that $PQ=P_1Q$ and $PR=P_2R$, so the perimeter ($\mathcal{P}$, say) of triangle $PQR$ is

\[\mathcal{P}\equiv P_1Q + QR + RP_2.\]

When $P_1$ and $P_2$ are fixed (equivalent to fixing $P$), the minimum of this sum is obtained when $P_1$, $Q$, $R$ and $P_2$ are collinear. In other words, the smallest value of $\mathcal{P}$ is the distance between $P_1$ and $P_2$ (shown as the dashed red line in the second sketch below). The intersection of $P_1P_2$ with $AB$ provides the optimal location of $Q$, while the intersection of the same line with $AC$ yields the optimum placement of $R$.

We are not quite done with the solution because the position of $P$ is yet to be specified. We will show that $P$ must be the foot of the altitude from $A$ in order for $P_1P_2$ to have the shortest length. To this end, join $P_1$ and $A$, as well as $P_2$ and $A$. The triangle $P_1AP_2$ is isosceles since

\[AP_1 =AP\quad\mbox{and}\quad AP=AP_2. \tag{1}\]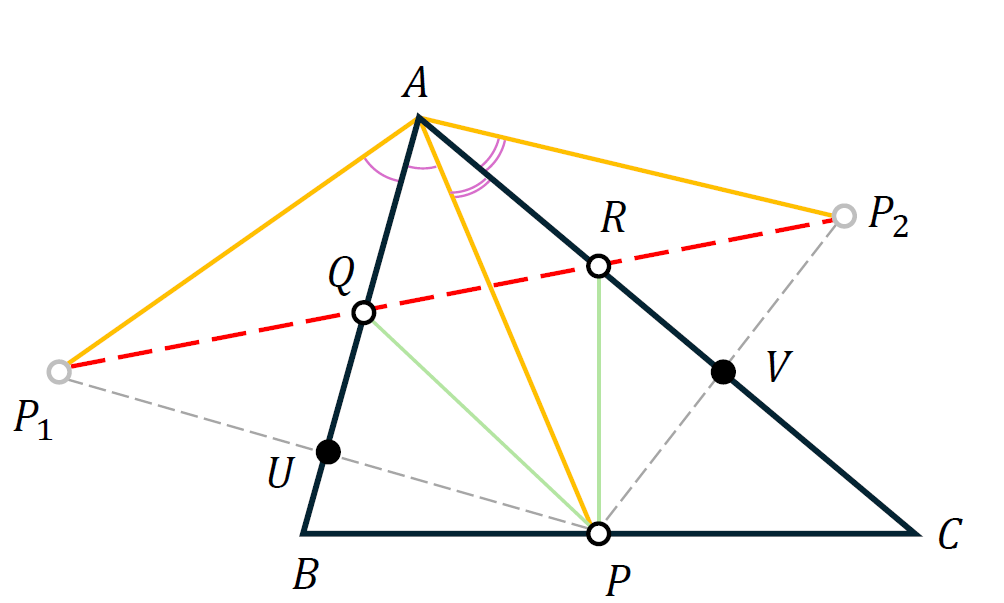

Furthermore, $\angle{P_1AP_2}$ is twice $\angle{BAC}$, i.e. it is independent of where $P$ is situated on $BC$. This observation suggests that the length of the side $P_1P_2$ will be the smallest possible when the length of $P_1A=P_2A$ is minimal; according to (1) this requires that $AP$ should also be as small as possible. This can only happen if $P$ is the foot of the perpendicular from $A$ to $BC$.

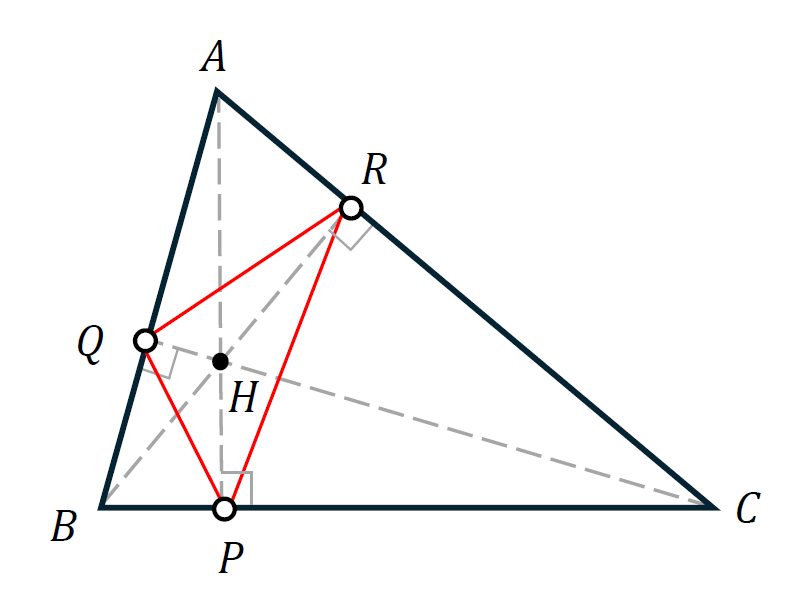
We can repeat the above arguments for $R$ and $Q$ to find that $CQ\perp AB$ and $BR\perp AC$. In conclusion, the solution to the original problem is the orthic triangle (also known as the altitude triangle).

Final remarks

While we have found the answer to the original problem, nothing was said about the value of the actual minimum perimeter. It is a routine exercise in trigonometry to show that the perimeter of the orthic triangle is

\[\mathcal{P}_{min} = \dfrac{r}{R}(a+b+c), \tag{2}\]

where $a$, $b$, and $c$ represent the lengths of the sides $BC$, $AC$ and $AB$, respectively, $r$ is the radius of the incircle, and $R$ denotes the radius of the circumcircle.

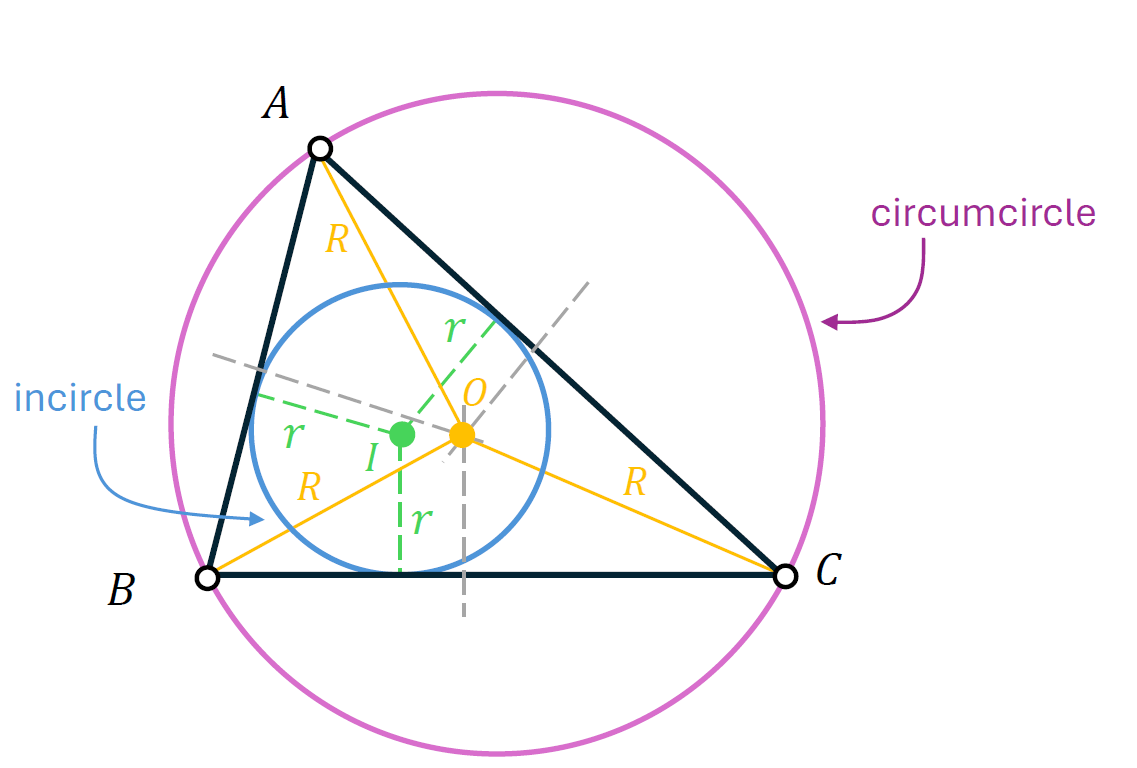
If we choose the vertices of the inscribed triangle to coincide with the mid-points of the corresponding sides of $\Delta{ABC}$, we get that its perimeter is simply $(a+b+c)/2$. Taking into account (2) and the minimum property of the orthic triangle we re-discover Euler’s inequality

\[R\geq{2r}.\]

Euler’s original proof of this remarkable result was based on calculating the distance between $I$ and $O$, the centres of the incircle and the circumcircle, respectively, $0\leq IO^2 = R(R-2r)$.

The solution of the milkmaid problem is not quite complete. We know that the optimal route, from the cow to the river and then to the farmhouse, would ideally mirror the path of a reflected ray of light. However, in practical terms, this information proves to be of limited assistance. Presumably, the milkmaid has access to a GPS device, and she knows the coordinates of her current location as well those of the farmhouse. We can safely assume that she has information about the location of the river (e.g., she knows the equation of the straight blue line we used earlier in this post). We will now work out the coordinates of the point $R_0$ on the bank of the river that she has to reach.

Let $(m_1,m_2)$ be the coordinates of the milkmaid (point $M$), let $(f_1,f_2)$ be the coordinates of the farmhouse (point $F$), and assume that the river is a straight line described by the equation $D(x,y)=0$, where

\[D(x,y) \equiv ax+by+c,\]

for some known values $a$, $b$, $c\in\mathbb{R}$.

First, we need the coordinates of $M_0$, the reflection of $M$ in the line that corresponds to the river. We will use the following result⁶:

Proposition: Let $(\alpha,\beta)$ be a point in $\mathbb{R}^2$. Its reflection in the line $y=px+q$ ($p$, $q\in\mathbb{R}$) is the point $(\widehat{\alpha},\widehat{\beta})$, where

\[\begin{aligned} &\widehat{\alpha} := \dfrac{(1-p^2)\alpha + 2p(\beta-q)}{1+p^2},\\ &{}\\ &\widehat{\beta} := \dfrac{-(1-p^2)\beta + 2p\alpha+2q}{1+p^2}. \end{aligned}\]

Although our line has a slightly different equation, it is clear that $p\equiv -a/b$ and $q\equiv -c/b$, so we can still apply this result to obtain the coordinates of $M_0$, which will be denoted by $(\widehat{m}_1,\widehat{m}_2)$.

The equation of the line $M_0F$ can be stated in parametric form

\[x = f_1 + t(\widehat{m}_1-f_1)\quad\mbox{and}\quad y = f_2 + t(\widehat{m}_2-f_2),\quad(t\in\mathbb{R}). \tag{3}\]

Substituting these expressions in the equation of the river, $D(x,y)=0$, we find that

\[t = -\dfrac{D(f_1,f_2)}{D(\widehat{m}_1,\widehat{m}_2)-D(f_1,f_2)}.\]

With this value of $t$ back into (3) we get the coordinates of the intersection point ($R_0$) between $M_0F$ and the river. Denoting these coordinates as $(x_0,y_0)$, it follows immediately that

\[\begin{aligned} &x_0 = \dfrac{f_1D(\widehat{m}_1,\widehat{m}_2)-\widehat{m}_1D(f_1,f_2)}{D(\widehat{m}_1,\widehat{m}_2)-D(f_1,f_2)},\\ &{}\\ &y_0 = \dfrac{f_2D(\widehat{m}_1,\widehat{m}_2)-\widehat{m}_2D(f_1,f_2)}{D(\widehat{m}_1,\widehat{m}_2)-D(f_1,f_2)}. \end{aligned}\]

At this stage, the milkmaid possesses all the necessary information to return to the farmhouse as swiftly as possible.

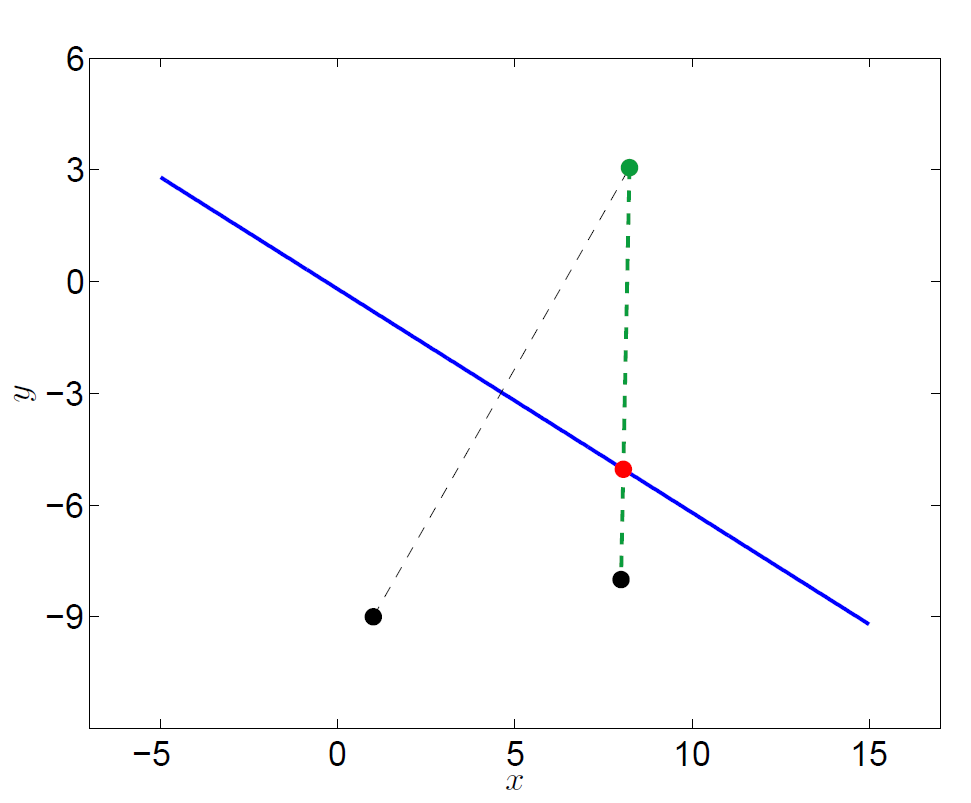
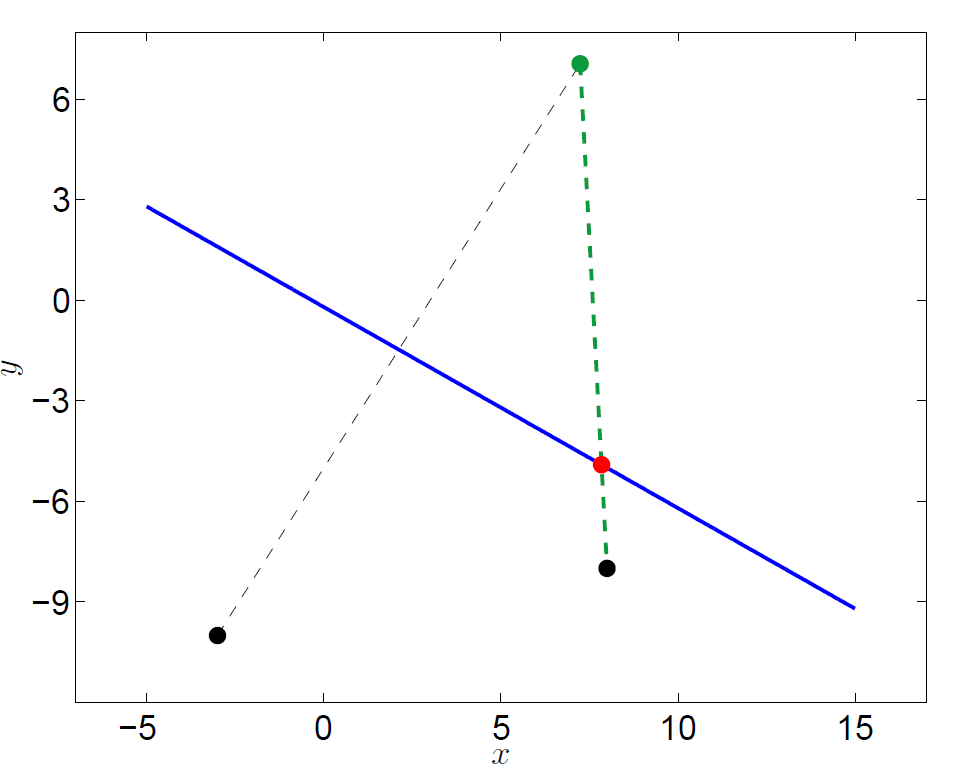
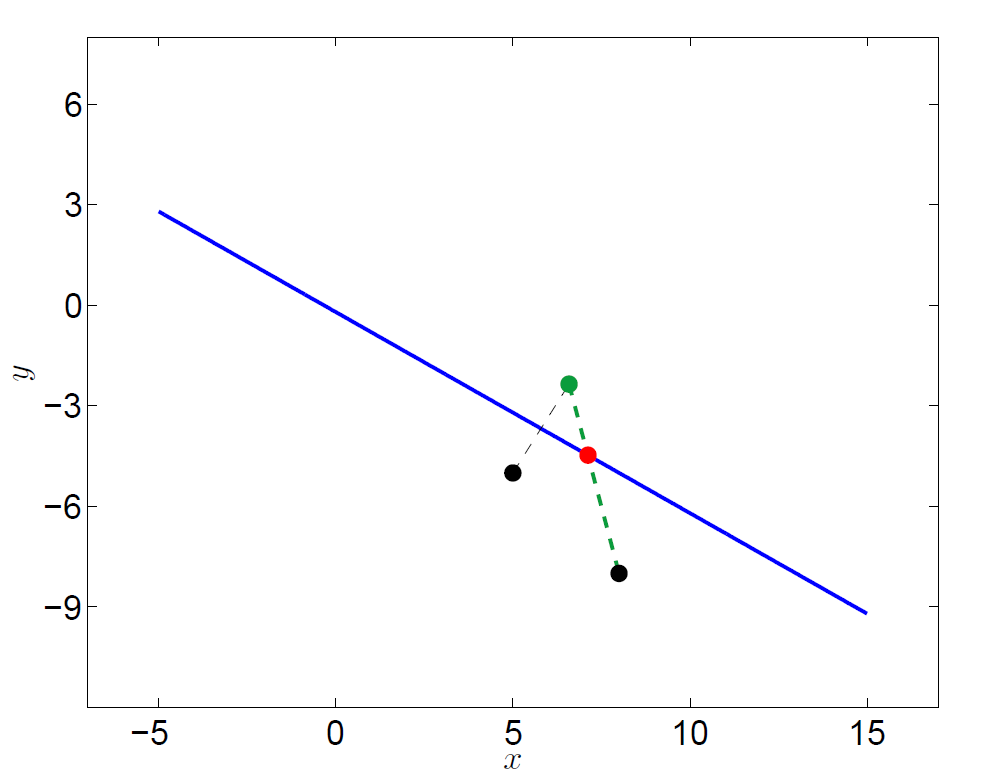
To check these calculations, I’ve plotted in MATLAB the results of the various formulae used above. There are three tests included below. The farmhouse had coordinates $(8,-8)$, and consecutively, the maid was placed at $(1,-9)$, $(-3,-10)$, and $(5,-5)$. The intersection point (shown in red) was calculated using the formulae for $x_0$ and $y_0$ stated above, and then $M_0$ and $F$ were also joined by a line to ensure that the calculated intersection was correct.

Footnotes

1. Walker, M.: Conjugate Functions for Engineers, Oxford University Press (1933). ↩

2. Weber, H.J., Arfken, G.B.: Essential Mathematical Methods for Physicists, Elsevier (2004). ↩

3. Gamelin, T.W.: Complex Analysis, Springer (2001). ↩

4. Palka, B.P.: An Introduction to Complex Function Theory, Springer-Verlag (1991). ↩

5. Dudeney, H.E.: Amusements in Mathematics, Thomas Nelson & Sons (1917). ↩ ↩²

6. Andreescu, T., Andrica, D.: Complex Numbers from A to… Z. Birkhausser, Boston (2005). ↩