Does shape matter?
Intro
In short, the answer is ‘yes.’ I am referring to storage tanks, like the ones depicted below, which are prevalent across various engineering fields. Chemical engineers frequently encounter the task of calculating the duration needed for a storage tank to drain completely. This post will explore how applied mathematics can help with tasks such as this. Of particular interest here will be finding the amount of time required to empty tanks of three distinct shapes: conical, cylindrical, and (hemi)spherical.
Differential equations play a key role in the realm of chemical engineering, particularly in scenarios involving fluid dynamics and process control. In the context of the aforementioned problem these equations are essential. Ordinary and partial differential equations (ODEs and PDEs, for short) are often derived from physical principles (e.g., conservation of mass, linear momentum, etc). These equations describe the rate of change of the fluid level or volume with respect to time. By considering the geometry of the tank, the fluid properties, and the outlet’s dimensions, one can formulate mathematical models that describe the fluid flow, enabling accurate predictions of the time taken for the tank to drain under various conditions.
While our main goals below are rather modest, the strategy used for dealing with this problem is representative of a much wider class of scenarios. We aim to illustrate how rates of change crop up naturally in physical problems.

A conical tank
Consider a conical tank like the one seen in the sketch below. The tank is initially filled with a non-viscous fluid (e.g., like water). At the lower end of the tank there is a cylindrical pipe that allows the liquid to escape out.
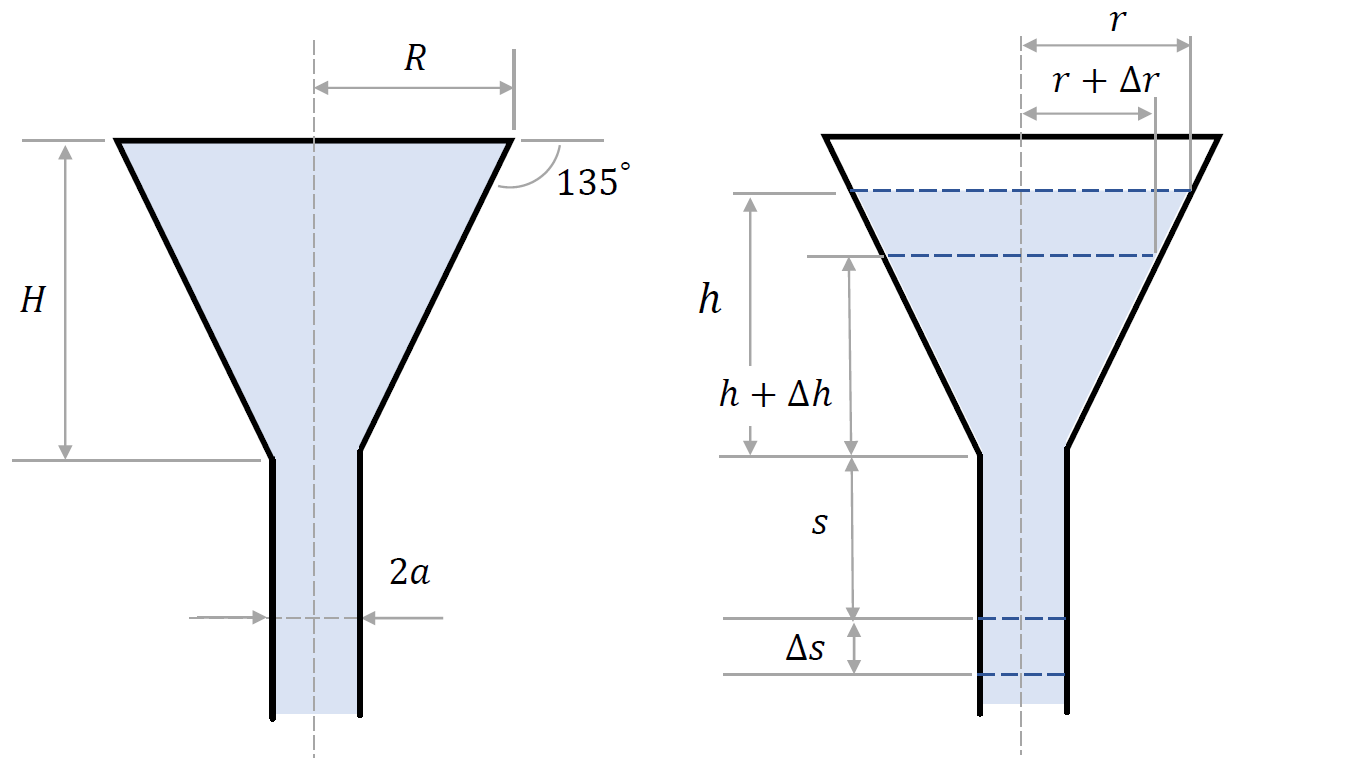
In a time interval from $t$ to $t+\Delta{t}$, the surface of the liquid (of uniform density $\rho$) falls from a height $h$ to a height $h+\Delta{h}$. The corresponding volume of liquid enters the drainpipe and occupies a cylindrical region of height $\Delta{s}$ and radius $0 < a < R$. The volume of liquid, $V$ (say), in the (truncated) conical section is a function of time; the same goes for the radius of the free surface of the liquid, i.e. $r=r(t)$.
\[\begin{aligned}[t] &V(t) = \dfrac{\pi}{3}r^3(t)-V_0,\\ &{}\\ &V(t+\Delta{t}) = \dfrac{\pi}{3}r^3(t+\Delta{t})-V_0. \end{aligned}\]At each instant of time the liquid fills up a variable spatial domain whose volume is the difference between the volumes of two different conical regions. One of them is fixed (i.e., independent of time), and its volume was denoted by $V_0$ in the above equations (note that $V_0=\pi a^3/3$, but this value is irrelevant in the subsequent developments).
Taking the difference of these two equations we find
\[V(t)-V(t+\Delta{t}) = \dfrac{\pi}{3}\left[r^3(t)-r^3(t+\Delta{t})\right]. \tag{1}\]Intuitively, it should be clear that a liquid such as water is incompressible; this means that the change of volume in the conical part must match the corresponding change in the cylindrical pipe (within a given arbitray interval of time $\Delta{t}$). The latter change of volume is $\pi{a^2}\Delta{s}$, so we can express the equality of the volume change as
\[V(t)-V(t+\Delta{t}) = \pi{a^2}\Delta{s}. \tag{2}\]Comparing (1) and (2) we can equate the right-hand sides of those two equations (see footnotes); after cancelling out the common factor ($\pi$) and dividing by $\Delta{t}$, we discover that
\[\dfrac{r^3(t+\Delta{t})-r^3(t)}{\Delta{t}} = -3a^2\dfrac{\Delta{s}}{\Delta{t}}.\]In the limit $\Delta{t}\to{0}$, the last equation reduces to
\[\dfrac{d}{dt}\left[r^3(t)\right]=-3 a^2v(t)\quad\Longrightarrow\quad 3r^2\dfrac{dr}{dt}=-3a^2v, \tag{3}\]where $v=ds/dt$ is the velocity of efflux, and in the last equation we have left out the dependence on $t$ (to simplify the notation).
Provided that the orifice is in a flat bottom, the velocity of efflux of a non-viscous fluid from a tank of otherwise arbitrary shape is know to be $v=\sqrt{2gh}$, where $g\simeq 10$ $m/s^2$ (the usual gravitational acceleration), and $h=h(t)$ is the depth of the liquid. This result is a consequence of Bernoulli’s principle. Note that because of the $45^\circ$ angle (i.e., $180^\circ-135^\circ$), we know that $h=r-a$. Using the information in (3) yields
\[r^2\dfrac{dr}{dt} = -a^2\sqrt{2g(r-a)}, \tag{4}\]which represents a separable ODE for the unknown function $r=r(t)$. In order to solve it we will also need the initial condition
\[r(0) = R. \tag{5}\]The general solution of (4) can be easily identified once we separate the variables $r$ and $t$ as indicated below
\[\dfrac{r^2}{\sqrt{r-a}}dr = -a^2\sqrt{2g}dt\quad\Longrightarrow\quad \int\dfrac{r^2}{\sqrt{r-a}}dr = -a^2\sqrt{2g}\int dt.\]The integral on the right-hand side of this last equation is simply $-a^2\sqrt{2g}(t+C)$, with $C\in\mathbb{R}$ the usual integration constant. To evaluate the integral on the left-hand side we introduce the substitution $u:=r-a$, so that $r=a+u$ and $dr = du$. Note that expressed in terms of $u$ the integral becomes
\[\int\dfrac{(a+u)^2}{\sqrt{u}}du = a^2\int u^{-1/2}du + 2a\int u^{1/2} du + \int u^{3/2} du.\]Each individual term can be routinely evaluated using the power-rule for integrals, thus leading to
\[u^{1/2}\left(2a^2 + \dfrac{4au}{3} + \dfrac{2u^2}{5}\right).\]Recalling that $u=r-a$, as well as the expression for the integral in $t$, we eventually arrive at an implicit solution for equation (4)
\[\dfrac{\sqrt{r-a}}{15}\left[16a^2+8ar(t)+6r^2(t)\right] = -a^2\sqrt{2g}(t+C); \tag{6}\]for our immediate purposes there is no need to take this expression further.
The integration constant is fixed by writing the above solution at $t=0$ and using the initial condition (5),
\[C = -\dfrac{2\sqrt{R-a}}{15a^2\sqrt{2g}}(8a^2+4aR+3R^2).\]If $t_{* }$ denotes the time it takes for emptying the tank, it should be clear that this is characterised by the condition $r(t_* )=a$. With $t\to t_{* }$ in (6), it follows that $t_{*} = C$ or
\[t_* = \dfrac{2(8a^2+4aR+3R^2)}{15a^2}\sqrt{\dfrac{R-a}{2g}}. \tag{7}\]Although we have solved the problem, the final result turns out to be a relatively complicated expression that depends on the parameters $a$ and $R$ ($g$ is just a physical constant, i.e. a concrete number). Ideally, we would like to have $t_{* }$ expressed in a simpler form. This can be achieved by introducing some suitable non-dimensional quantities. Notice that if $a$ is measured in metres, then the ratio $a/g$ will be measured in seconds squared, and hence $(a/g)^{1/2}$ will be measured in seconds. We are therefore prompted to consider the following dimensionless quantities
\[\tau_{cone}:=t_* \left(\dfrac{a}{g}\right)^{-1/2},\quad \eta:=\dfrac{R}{a}>1.\]Expressed in terms of these rescaled variables equation (7) assumes the form
\[\boxed{\tau_{cone} = \dfrac{1}{15}(8+4\eta+3\eta^2)\sqrt{2(\eta-1)}.} \tag{8}\]Cylindrical tank
If the cone is replaced with a cylinder, the problem of finding the time needed to empty the tank is much simpler because now $r(t)$ in the previous scenario will be constant for all $t\geq{0}$. We consider the system seen below; the definitions of the various quantities needed subsequently are indicated on the sketch.
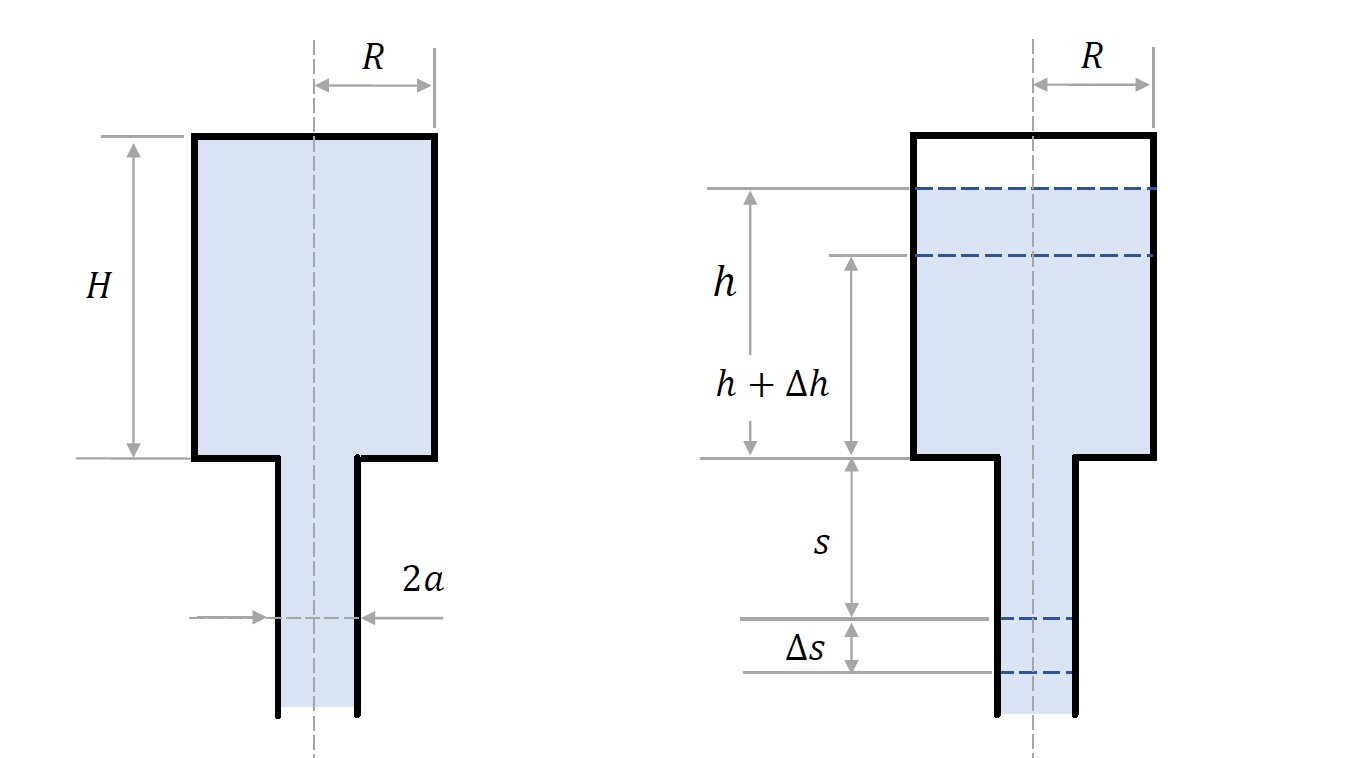
For the volume $V$ of the fluid in the cylindrical upper part we can write
\[\begin{aligned}[t] &V(t) = \pi{R^2}h(t),\\ &{}\\ &V(t+\Delta{t}) = \pi{R^2}h(t+\Delta{t}). \end{aligned}\]The change of volume in the drainpipe remains consistent with what we have already seen earlier. By proceeding in exactly the same way as before, it is found that
\[\pi{R^2}\left[\dfrac{h(t+\Delta t)-h(t)}{\Delta t}\right] = -\pi{a^2}\dfrac{\Delta s}{\Delta t},\]while in the limit $\Delta t\to{0}$ this becomes
\[R^2\dfrac{dh}{dt} = -a^2 v\quad\Longrightarrow\quad R^2\dfrac{dh}{dt} = -a^2\sqrt{2gh}.\]The last equation is easily recognised as being another separable ODE, which we re-arrange and then integrate
\[\dfrac{dh}{\sqrt{h}}= -\sqrt{2g}\left(\dfrac{a}{R}\right)^2 dt \Longrightarrow \int\dfrac{dh}{\sqrt{h}}= -\sqrt{2g}\left(\dfrac{a}{R}\right)^2\int dt.\]The general solution turns out to be
\[\sqrt{h(t)} = -\dfrac{1}{2}\left(\dfrac{a}{R}\right)^2\sqrt{2g} t + C,\qquad (C\in\mathbb{R}).\]The integration constant $C$ is fixed by considering the initial condition $h(0)=H$, whence $C = \sqrt{H}$; the equation immediately above becomes
\[\sqrt{h(t)} = -\dfrac{1}{2}\left(\dfrac{a}{R}\right)^2\sqrt{2g} t + \sqrt{H}. \tag{9}\]The draining time $t_{* }$ is identified by the condition $h(t_{* }) = 0$; to take advantage of this information we need to set $t\to t_{* }$ in (9), which results in
\[t_* = \dfrac{\sqrt{2gH}}{g}\left(\dfrac{R}{a}\right)^2. \tag{10}\]Finally, by introducing $\tau_{cyl}:=t_{* }(a/g)^{-1/2}$ and $\eta:=R/a>1$, equation (10) can be stated in the form
\[\boxed{\tau_{cyl} = \sqrt{2}\left(\dfrac{H}{a}\right)^{1/2}\eta^2.} \tag{11}\]Hemispherical tank
Having worked through the solutions for the conical and cylindrical tanks, it will perhaps come as no surprise that we can still follow a similar strategy for a hemispherical configuration. However, the volume of a spherical cap is slightly more involved than the expressions we have encountered thus far. Before we get started we recall that this volume can be expressed in two different ways
\[V = \dfrac{1}{6}\pi h (3a^2+h^2) = \dfrac{1}{3}\pi h^2(3R-h), \tag{12}\]where $a$ and $h$ are indicated in the sketch below.
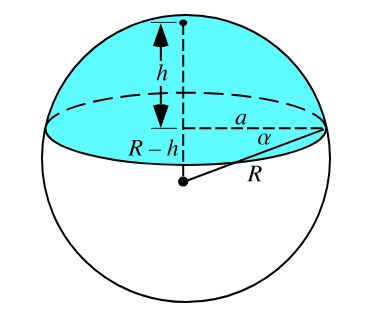
For our immediate purposes it will be convenient to use the latter expression (since $R$ is constant, so there is just one time-dependent quantity, $h=h(t)$, in (12)).
The setup we are going to be interested in is illustrated below.
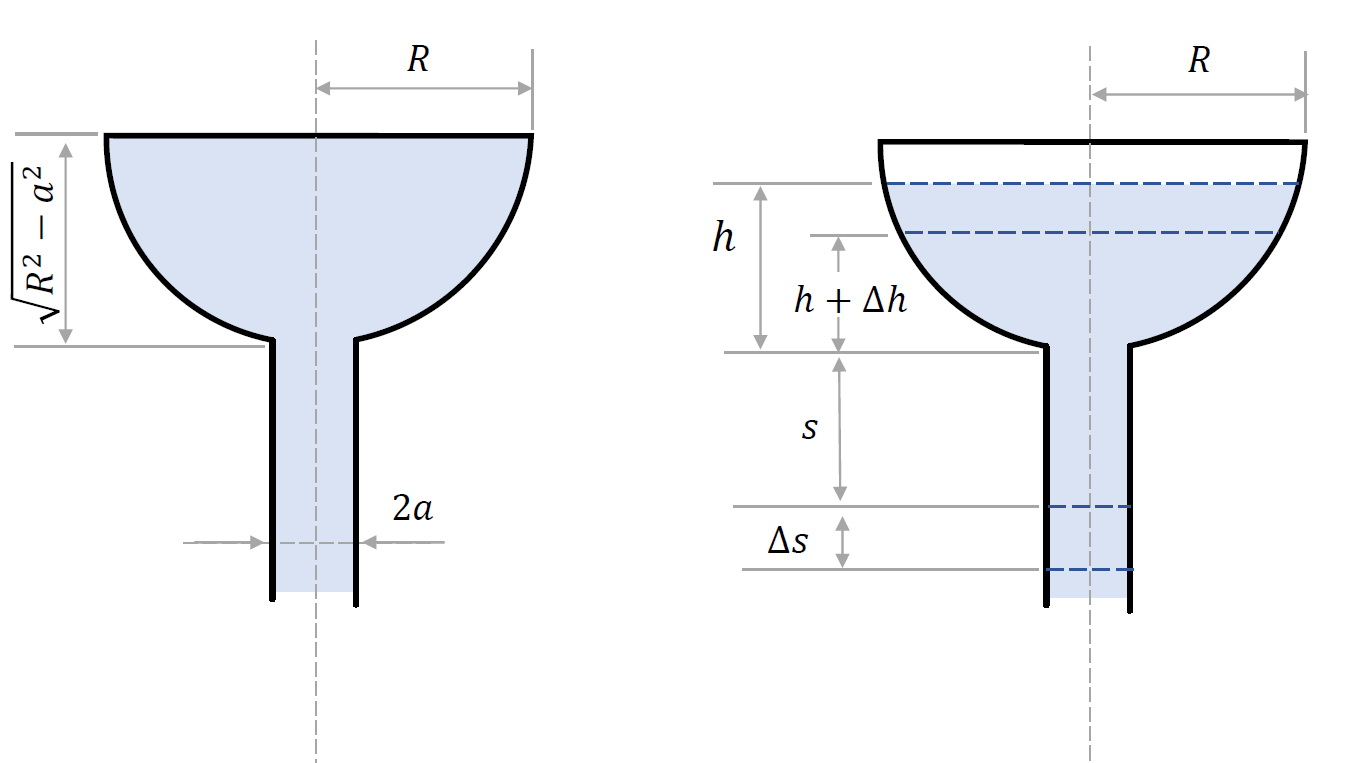
The volume of liquid in the spherical tank is expressed at two neighbouring instants of time, $t$ and $t+\Delta{t}$, respectively,
\[\begin{aligned}[t] &V(t) = \pi R h^2(t) - \dfrac{1}{3}\pi h^3(t)-V_0,\\ &{}\\ &V(t+\Delta{t}) =\pi R h^2(t+\Delta t) - \dfrac{1}{3}\pi h^3(t+\Delta t)-V_0, \end{aligned}\]where $V_0$ is the constant volume of the spherical cap whose base radius is $a$ (at this stage we do not need this quantity).
The volume in the cylindrical drainpipe is calculated exactly as before. Constructing the difference quotient for $V$ in a similar manner, and then letting $\Delta\to{0}$, it transpires that
\[\begin{aligned}[t] &\dfrac{dV}{dt} = \pi R\dfrac{d}{dt}\left(h^2\right)-\dfrac{\pi}{3}\dfrac{d}{dt}\left(h^3\right)\\ &{}\\ &{}\qquad = -\pi a^2 v = -\pi a^2\sqrt{2gh}. \end{aligned}\]Next, we manipulate the above differential equation for $h(t)$ in order to separate the variables and identify its solution
\[\begin{aligned}[t] &2R h\dfrac{dh}{dt}- h^2\dfrac{dh}{dt} = -a^2\sqrt{2gh}\\ &{}\\ &\quad\Longrightarrow\quad h(2R-h)\dfrac{dh}{dt} = -\left(a^2\sqrt{2g}\right) h^{1/2}\\ &{}\\ &\quad\Longrightarrow\quad \dfrac{h(2R-h)dh}{h^{1/2}} = -\left(a^2\sqrt{2g}\right) dt\\ &{}\\ &\quad\Longrightarrow\quad (2Rh^{1/2}-h^{3/2})dh = -\left(a^2\sqrt{2g}\right) dt\\ &{}\\ &\quad\Longrightarrow\quad 2R\int h^{1/2}dh-\int h^{3/2}dh = -a^2\sqrt{2g}\int dt. \end{aligned}\]Again, the two integrals on the left-hand side in the last equation are easily calculated, and the final result turns out to be an implicit solution,
\[\dfrac{2h^{3/2}}{3}\left(2R-\dfrac{3h}{5}\right) = -\left(a^2\sqrt{2g}\right) t + C,\quad (C\in\mathbb{R}). \tag{13}\]The integration constant is readily available from the initial condition
\[h(0) = \sqrt{R^2-a^2} = a\sqrt{\eta^2-1},\qquad \eta:=\dfrac{R}{a}.\]Setting $t=0$ in (13) yields
\[C = \dfrac{2}{3}a^{5/2}(\eta^2-1)^{3/4}\left[2\eta-\dfrac{3}{5}(\eta^2-1)^{1/2}\right].\]When the tank is empty, i.e. at some instant of time $t=t_{* }$, the height of the liquid in the spherical part is zero or $h(t_{* })=0$. This leads to $t_{* }=C/(a^2\sqrt{2g})$ or, after introducing the non-dimensional quantity $\tau_{sph}:=t_*(a/g)^{-1/2}$, we find
\[\boxed{\tau_{sph} = \dfrac{\sqrt{2}}{3}(\eta^2-1)^{3/4}\left[2\eta-\dfrac{3}{5}(\eta^2-1)^{1/2}\right].} \tag{12}\]Discussion
It is time to take a closer look at the results obtained above. We cannot compare directly the formulae (8), (11), and (12) because the corresponding storage tanks do not have the same volume (note that $\eta$ in the three formulae is based on $R$, which has different connotation in each of three cases considered). The correct approach to tackle this is demonstrated shortly for comparing the draining times concerning conical and (hemi)spherical shapes.
For the sake of clarity, let $R_1$ denote the corresponding $R$ for the cone, and $R_3$ the radius of the sphere in the last example. If the volumes of the two shapes is the same, then
\[\dfrac{1}{3}\pi R_1^3 -\dfrac{1}{3}\pi a^3 = \dfrac{2}{3}\pi R_3^3-\dfrac{1}{3}\pi h_0^2(3R_3-h_0), \tag{13}\]where $h_0:=R_3-\sqrt{R_3^2-a^2}$. If we let $\eta_1:=R_1/a$ and $\eta_3:=R_3/a$, further manipulations of equation (13) show that
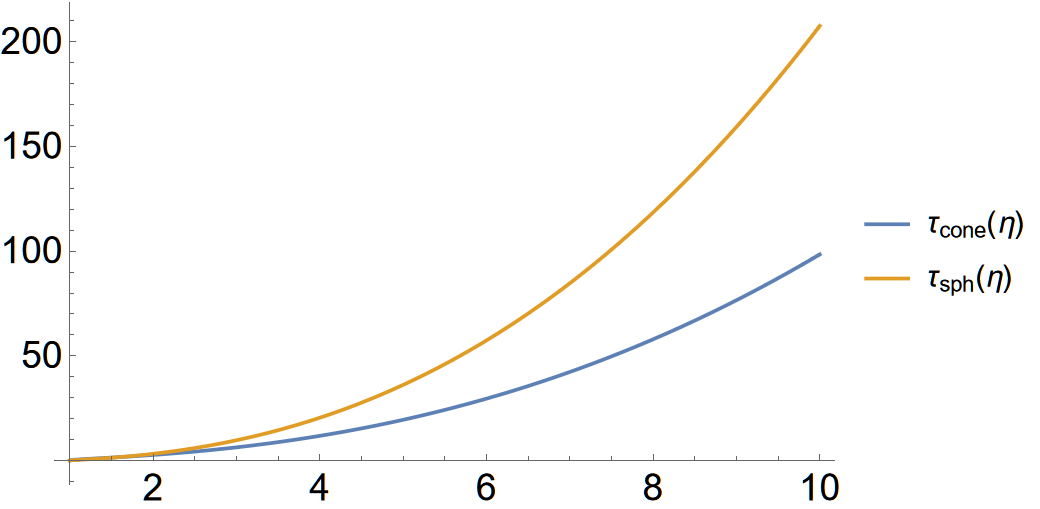
\[\eta_1^3 = 1+2\eta_3^3-\left(\eta_3-\sqrt{\eta_3^2-1}\right)^2\left(2\eta_3+\sqrt{\eta_3^2-1}\right).\]This suggests that in (8) we need to make the substitution $\eta\to\eta_1$, where $\eta_1$ is related to $\eta_3$ by the above algebraic relation; we can then compare $\tau_{cone}$ to $\tau_{sph}$ as they correspond to the same volume of liquid. One such comparison is included in the first plot below, where on the horizontal axis we use $\eta\to\eta_3$ that appears on the right-hand side of (13). It is clear that the conical shape performs better than the hemispherical container (this is true for $\eta>1.6$).
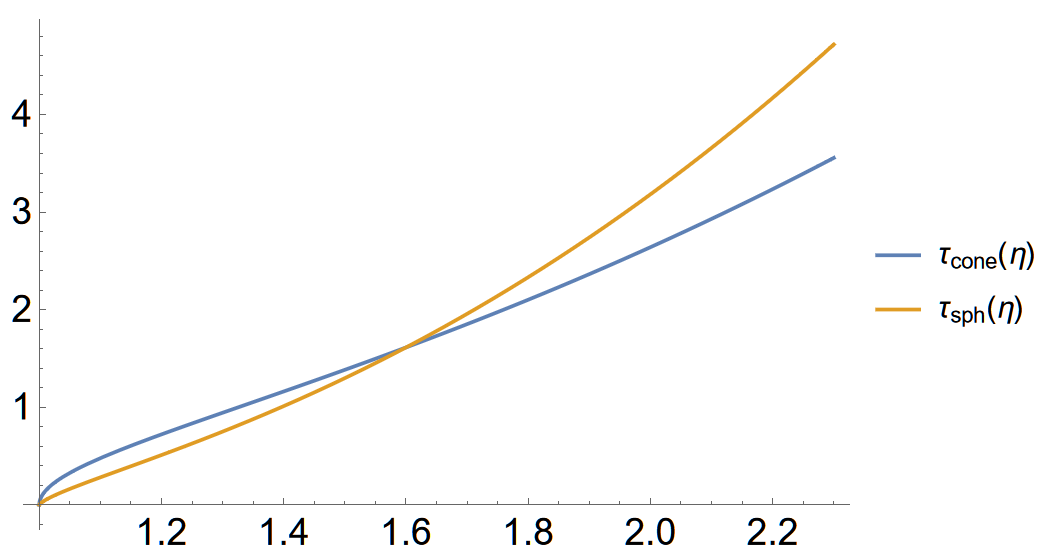
However, if we zoom in, we notice that for $\eta$ between $1$ and $1.6$ the spherical tank would appear to be more efficient (see the second plot below). This amounts to configurations for which $a < R < 1.6a$, which is an unlikely scenario in practice.
To make things simple, we have assumed an angle of $45^\circ$ for the original cone; this results in the height of the cone being equal to its height (a significant simplification). However, this assumption can be relaxed by considering an arbitrary angle $0^\circ < \alpha < 90^\circ$, and then finding its corresponding value that minimises $\tau_{cone}$. More about this, and other related aspects, in a future post.
The simple-minded results obtained above suggest some speculations about the conical shape of a typical funnel.

Of course, the conical design offers a practical solution to a variety of purposes, e.g. in directing and channeling substances efficiently. The wide mouth of the funnel allows for easy pouring of liquids without splashes or spilling. As the funnel narrows down into a cone, it controls the flow by directing the substance precisely where it needs to go. But according to our calculations it seems that the conical form of funnels also optimises the gravitational force acting on the substance being poured. Looking at the aspect ratios $R/a$ for a typical funnel (see the above pictures), it is clear that this tends to be significantly larger than $1.6$.
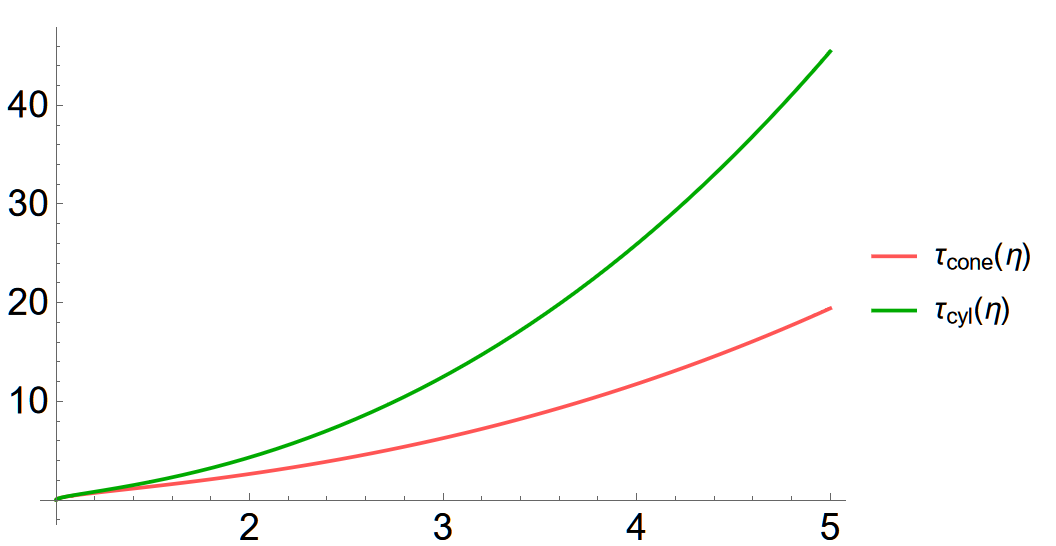
The formula for $\tau_{cyl}$ depends on two independent non-dimensional parameters, $\eta\equiv R/a$ and $H/a$, which means that a direct comparison with $\tau_{cone}$ requires the discussion of several cases. We will confine ourselves to the situation in which the radius of the cone is the same as that of the cylinder. If we represent these by $R_1$ and $R_2$, respectively, the aforementioned condition translates into $R_1=R_2$ or $R_1/a=R_2/a$ (i.e., the $\eta$-values mentioned in (8) and (11) are identical, and we designate their shared value as $\eta$). The equality of the volumes of the two corresponding storage tanks is
\[\dfrac{1}{3}\pi R_1^3 - \dfrac{1}{3}\pi a^3 = \pi R_2^2 H,\]whence
\[\dfrac{H}{a} = \dfrac{\eta^3-1}{3\eta^2}.\]Plugging this value into (11), we can then compare the result with (8) – see below.
Footnotes
The argument that led to the equality of the left-hand sides of equations (1) and (2) is known as the principle of mass conservation. If the density of a fluid (or a solid) is constant, then from the definition $\rho = m/V$ we get that $m = \rho{V}$, i.e. the mass of any closed region within the fluid is proportional to its volume. Therefore, if mass is conserved, the same must be true for volume. A more rigorous discussion can be found in this book.