Pizza party!

1. Intro
2. The problem
3. Areas in polar coordinates
4. A lemma
5. Solution
6. Vegan pizza
7. Another lemma
8. Discussion
9. Footnotes

Intro

This time of year it is all about food and the spirit of the festive season. Personally, I lean more towards the culinary delights, which inspired me to consider writing with a culinary theme. Picture this: you’re eager to share a pizza with your closest friend, both of you hungry and craving equal-sized slices. You might start cutting through the centre, and then proceed similarly to the diagram below:

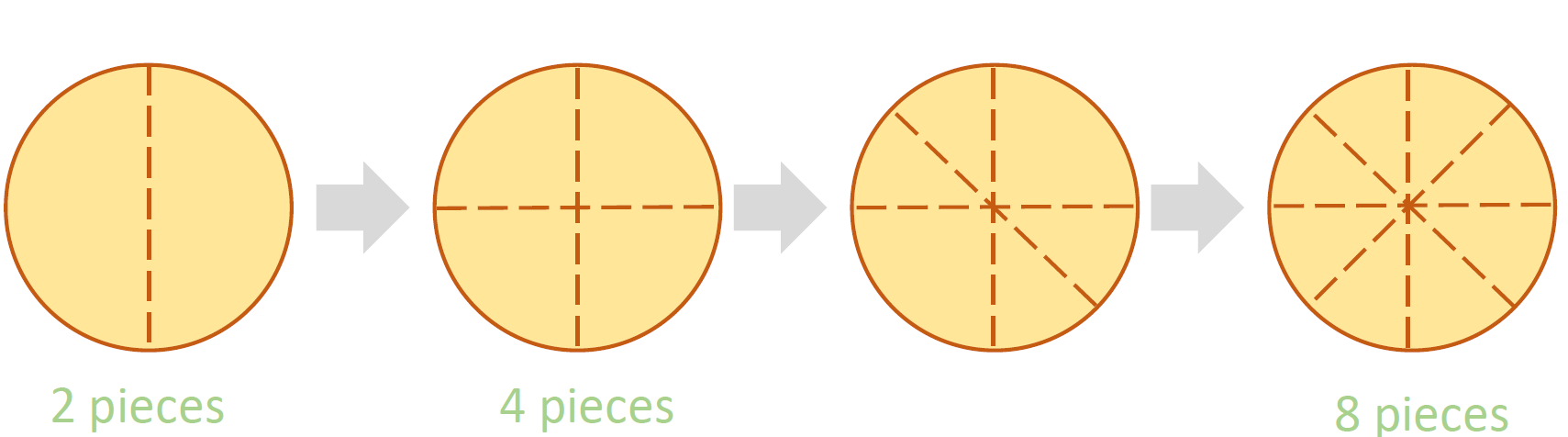
With a little stroke of luck, the outcome of this dilligent effort might resemble the pizza depicted in the next image:

However, is this the only way to equitably divide the pizza with your friend? Interestingly, it turns out that there are many other quick ways to slice your pizza unevenly, guaranteeing that both you and your friend receive an equal portion of food.

Let’s delve into a potential answer to the previous question. Our approach will follow the conventional method of applied mathematics: we will begin by translating the given scenario into precise mathematical language, and subsequently utilise various tools to gain deeper insights into the specific challenges posed by the situation.

[A note of caution: Always begin with lightweight tools such as “screwdrivers” and “calipers”; reserve the “sledgehammer” as a final option.]

The problem

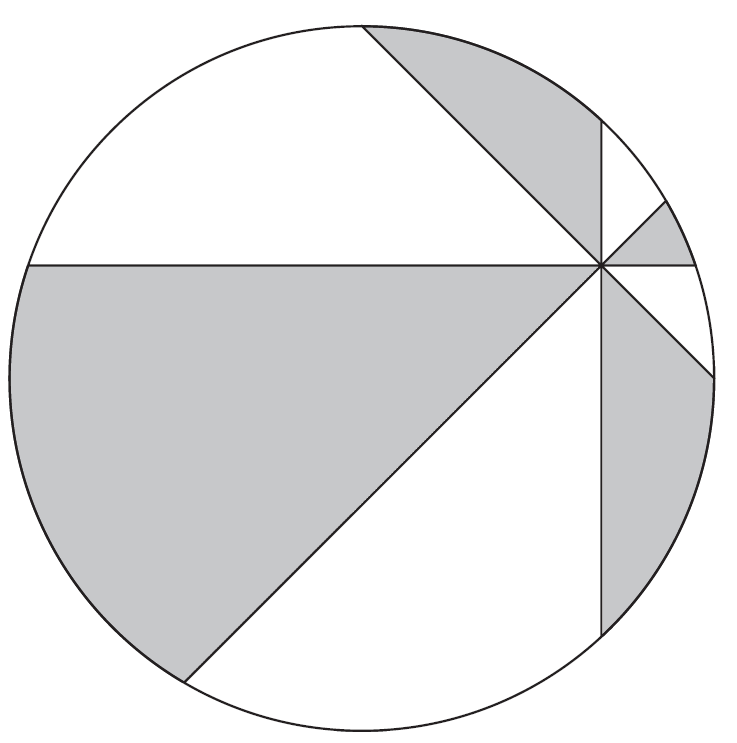
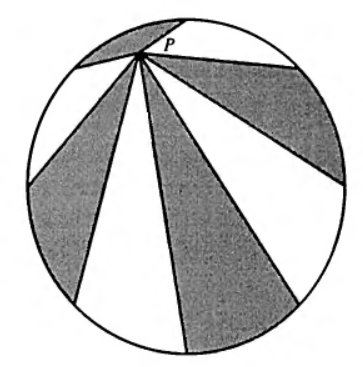
Through an arbitrary point inside a circle draw four chords making eight $45^\circ$ angles. Colour the resulting regions alternately black and white as seen in the sketch included below. Then, the total area of the black regions is the same as the total area of the white ones¹.

As we are going to see shortly, a simple result typically covered in first-year Calculus courses will come to our rescue. This is outlined next.

Areas in polar coordinates

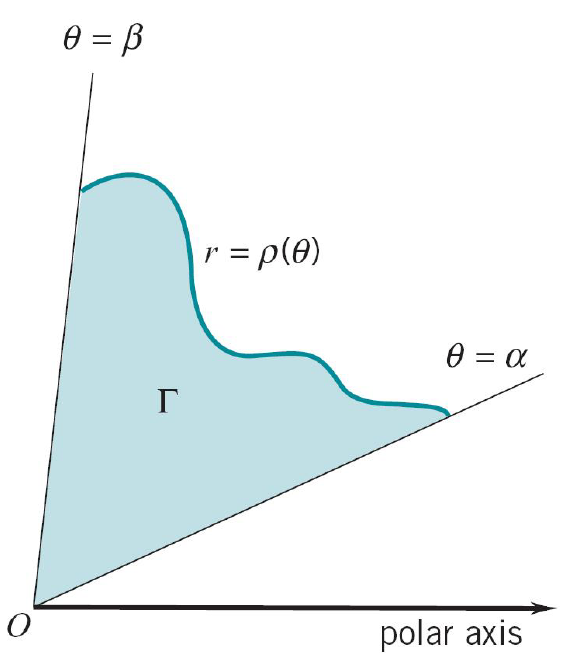
It is well known that the definite integral of a function $y=f(x)$ is typically associated with the “area below the graph” of the integrand. In many situations functions are more conveniently expressed in polar coordinates $(r,\theta)$. We recall below the formula for the area of a region the boundary of which is given in polar coordinates.

Suppose that $\alpha$ and $\beta$ are two real numbers with $\alpha<\beta\leq \alpha+2\pi$. We take $\rho(\theta)$ to be a continuous function on $[\alpha,\beta]$ that keeps a constant sign on this interval. We are interested in the area $A$ (say) of the polar region $\Gamma$ (see below) generated by the curve

\[r = \rho(\theta),\qquad\alpha\leq\theta\leq\beta.\]

The formula for this area is²

\[A = \dfrac{1}{2}\int_{\alpha}^{\beta}r^2(\theta) d\theta. \tag{1}\]

Note: If $\rho(\theta)$ were negative, the region $\Gamma$ would appear on the opposite side of the pole (i.e., the point $O$). The formula for the area of that region remains unchanged, i.e. it is still given by (1).

A lemma

The solution of the pizza problem is based on a simple auxiliary result¹:

Two perpendicular chords $MN$ and $ST$ in a circle of radius $R$ pass through an arbitrary point $P$ situated inside the circle (see the sketch included below). If $a$, $b$, $c$, $d$ denote the lengths of the segments $PS$, $PN$, $PT$, $PM$, respectively, then

\[a^2 + b^2 + c^2 + d^2 = 4R^2. \tag{2}\]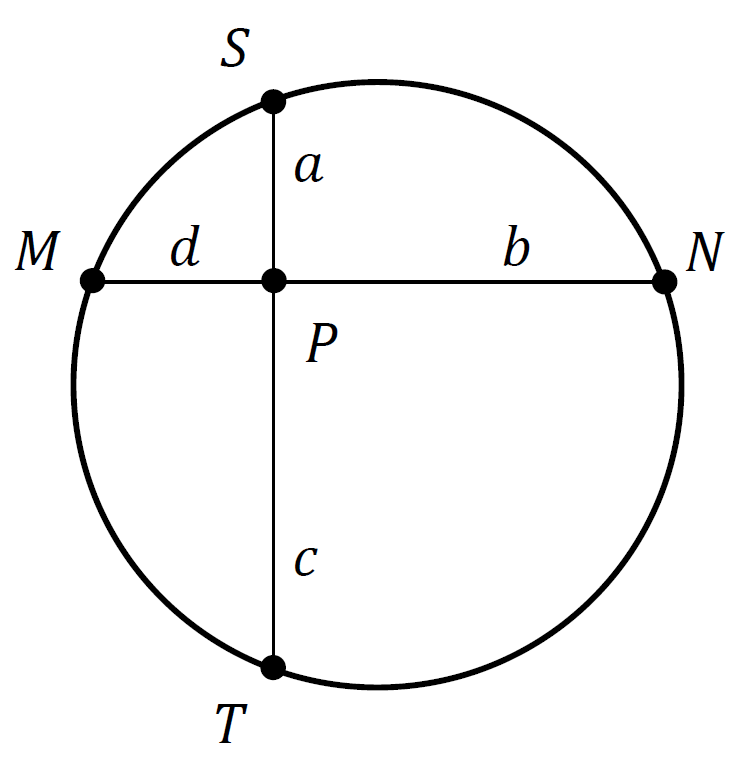

A possible solution can be given by constructing the diameter of the circle that passes through $M$; let $M’ $ be the point where $MO$ cuts the circle again – clearly, $MM’=2R$; refer to the sketch included below:

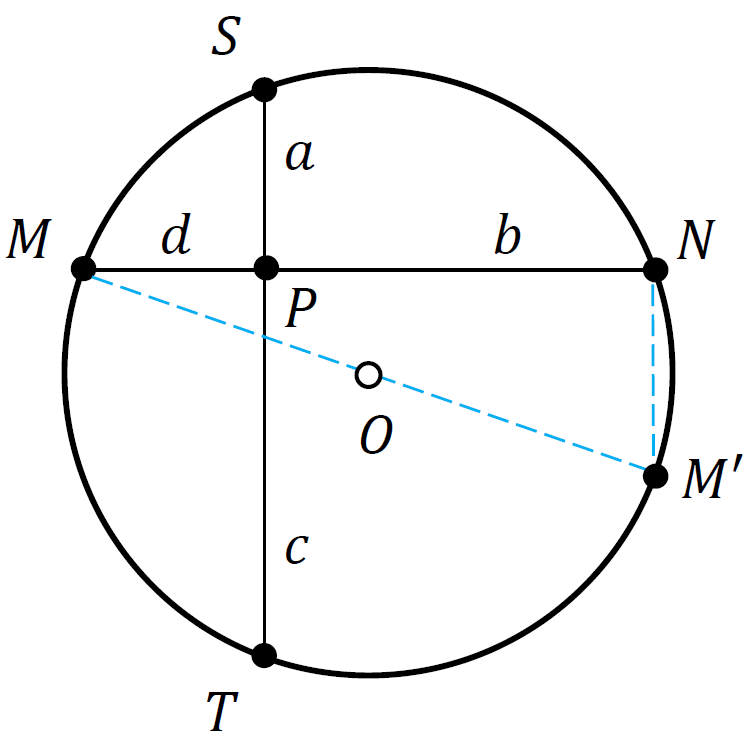
The line $M’N$ is perpendicular to $MN$ (since $\angle{MNM’}$ subtends a semicircle). This means that $NM’$ is parallel to $ST$ and $NM’=c-a$. The Pythagorean theorem applied to $\Delta{MNM’}$ gives

\[\begin{aligned}[t] &MM'^2 = MN^2+NM'^2\\ &{}\\ &\Longrightarrow\quad (2R)^2 = (b+d)^2 + (c-a)^2\\ &{}\\ &\Longrightarrow\quad 4R^2 = b^2+d^2+2bd + c^2+a^2-2ac. \end{aligned} \tag{3}\]

The power of point $P$ with respect to the given circle assures us that $PM\cdot PN = PS\cdot PT$ or $bd=ac$. Hence, the two rogue terms in (3) cancel out, and we are left with (2).

Solution

Without loss of generality we take $R=1$, and adopt a polar system of coordinates centred at $P$ and having one of the chords as its polar axis. With reference to the sketch at the top of this post, we choose the horizontal chord as the polar axis. The area of each black region can be expressed through an integral of the form (1) for suitably chosen $\alpha$ and $\beta$. Let’s denote each of these integrals by $I_k$, with $k=0,2,4,6$; the labelling is done counter-clockwise, starting from the first slice (for which $\alpha\to{0}$ and $\beta\to\pi/4$). Note that

\[\mbox{total black area} = I_0 + I_2 + I_4 + I_6, \tag{4}\]

where

\[I_k = \dfrac{1}{2}\int_{k\pi/4}^{(k+1)\pi/4}r^2(\theta)d\theta\,,\quad k=0,4,6,8.\]

It is possible to reduce the integration range to $[0,\pi/4]$ in each integral by making the change of variable

\[\theta = \dfrac{k\pi}{4}+\alpha,\quad k=2,4,6.\]

With this observation in mind, the sum (4) can be re-written as

\[\dfrac{1}{2}\int_0^{\pi/4}\left[r^2(\alpha)+r^2(\alpha+\pi/2)+r^2(\alpha+\pi)+r^2(\alpha+3\pi/2)\right]d\alpha. \tag{5}\]

Furthermore, $r(\alpha)$ and $r(\alpha+\pi)$ belong to a common chord, while $r(\alpha+\pi/2)$ and $r(\alpha+3\pi/2)$ form another chord perpendicular to the former; this holds true for all $\alpha\in[0,\pi/4]$. Invoking the above lemma – see (2), we conclude that (5) is equal to

\[\dfrac{1}{2}\int_0^{\pi/4} 4 d\alpha = \dfrac{1}{2}\times{4}\times\dfrac{\pi}{4} =\dfrac{\pi}{2},\]

which is half of the area of the circle (since $R=1$). This means that the total area of the white regions has the same value, and the proof is complete.

Vegan pizza

A lighter version¹ of the pizza problem goes as follows: Suppose $n>2$ is an even natural number, and consider $n$ equally spaced points on the circumference of a given circle; $P$ is an arbitrary point inside the circle. Join $P$ to each of the $n$ equidistant points and colour the resulting regions alternately black and white, as in the skecth included below (a particular scenario for $n=8$). Then, the total area of the black region is the same as that of the white region.

This variation of the original pizza problem is much simpler because we now know right from the outset the lengths of the arcs connecting any two consecutive points on the circle. That information was previously lacking (we knew only the angles between the chords). The area of each pizza “slice” (either black or white) consists of the area of a triangle together with an additional curvy part (a segment which is cut from the circle by a chord defined by the vertices situated on the circle). The areas of each segment is the same for all “slices” since the arcs are equal to each other. The common value of these areas is

\[\dfrac{1}{2}\left(\dfrac{2\pi}{n}-\sin\dfrac{2\pi}{n}\right),\]

where we have taken the radius of the circle to be $R=1$ (there is no loss of generality by making that assumption).

Taking this simple observation into account, we can confine ourselves to the areas of the standard triangles determined by $P$ and any two consecutive points along the circle (i.e., by disregarding the curvy parts). Those areas can be evaluated by using complex numbers. One of the key results is stated next.

Another lemma³⁴

The area of a directly oriented triangle $Q_1Q_2Q_3$ whose vertices have coordinates $z_1$, $z_2$, $z_3$ is

\[\mbox{area}(\Delta Q_1Q_2Q_3) = \dfrac{1}{2}\mbox{Im}\left(\overline{z}_1z_2 + \overline{z}_2z_3 + \overline{z}_3z_1\right), \tag{6}\]

where ‘Im($\dots$)’ represents the imaginary part of the expression enclosed within the brackets.

The phrase ‘directly oriented’ refers to where the region bounded by the triangle is situated as a caterpillar crawls along the sides of the triangle. If that region is on its left, then the orientation of the triangle is ‘positive’ (or ‘direct’); if it is on its right, then the triangle is said to be ‘negatively oriented’.

We will assume that $P$ has a complex coordinate $z=r e^{i\theta}$ with ${0 < r < 1}$ and $\theta\in [0,2\pi)$. As for the set of equidistant points on the circle, we will label them $A_k$ for $k=0,1,\dots,2m-1$, where $n=2m$ for some $m\in\mathbb{N}$ ($m\geq{2}$); the coordinates of these points are the $n$-th roots of unity

\[z_k = \exp\left(\dfrac{2k\pi i}{n}\right) = \exp\left(\dfrac{k\pi i}{m}\right),\quad k=0,1,\dots,\quad 2m-1.\]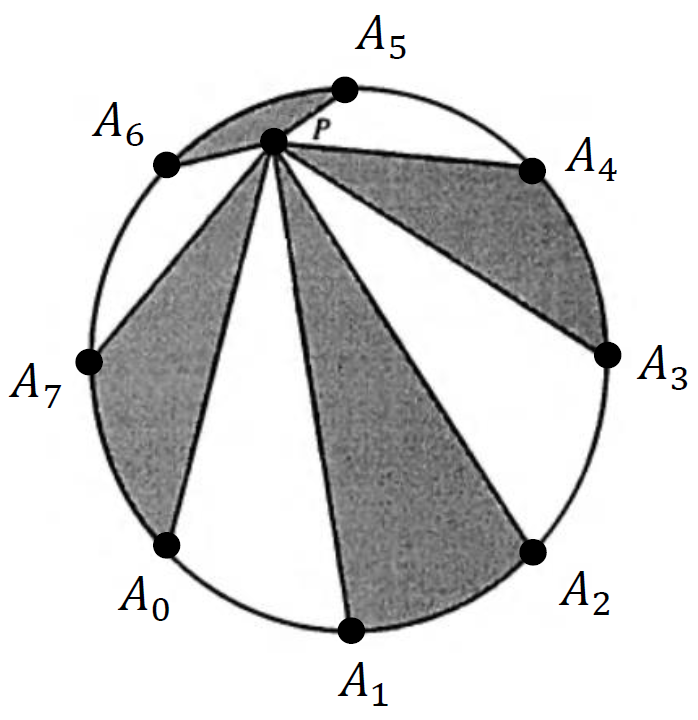

The colouring of the triangles is entirely arbitrary as long as we do it alternately. For the sake of definiteness, let’s assume that $\Delta{PA_0A_1}$ is white. We can then enumerate all the white triangles:

\[\Delta{PA_0A_1},\quad\Delta{PA_2A_3},\quad \Delta{PA_4A_5},\quad\dots,\quad\Delta{PA_{2m-4}A_{2m-3}}, \quad\Delta{PA_{2m-2}A_{2m-1}}.\]

(In the sketch above $m=4$.)

Using formula (6), the expressions whose imaginary parts we need to consider are

\[\begin{aligned}[t] &\overline{z}z_0 + \overline{z}_0z_1 + \overline{z}_1z,\\ &{}\\ &\overline{z}z_2 + \overline{z}_2z_3 + \overline{z}_3z,\\ &{}\\ &\overline{z}z_4 + \overline{z}_4z_5 + \overline{z}_5z,\dots\\ \end{aligned}\] \[\dots\dots,\] \[\begin{aligned}[t] &\overline{z} z_ {2m-4} + \overline{z}_ {2m-4} z_ {2m-3} + \overline{z}_ {2m-3} z,\\ &{}\\ &\overline{z}z_ {2m-2} + \overline{z}_ {2m-2} z_ {2m-1} + \overline{z}_ {2m-1}z. \end{aligned}\]

Adding up, the resulting expression can be written more compactly as

\[\overline{z}\left(\sum_{k=0}^{m-1}z_ {2k}\right)+\sum_{k=0}^{m-1}\overline{z}_ {2k}z_ {2k+1} +z\left(\sum_{k=0}^{m-1}\overline{z}_ {2k+1}\right).\]

Recall that we are actually interested only in the imaginary part of this, which is

\[\sum_{k=0}^{2m-1}(-1)^{k+1}\sin(\theta-\theta_k) + \sum_{k=0}^{m-1}\sin(\theta_ {2k+1}- \theta_ {2k}), \quad \theta_k\equiv\dfrac{k\pi}{m}\,. \tag{7}\]

The first sum above is zero (e.g., use mathematical induction), while the second one has a constant summand whose value is $\sin\theta_1$. In conclusion, (7) reduces to $m\sin(\pi/m)$, and the area we are after is half of this value – see (6). Hence, the total sum of the areas of the white triangles is

\[\dfrac{m}{2}\sin\left(\dfrac{\pi}{m}\right).\]

On the other hand, it is well known that the area of a regular $n$-sided polygon inscribed in a circle of radius $R=1$ is

\[\dfrac{n}{2}\sin\left(\dfrac{2\pi}{n}\right).\]

Comparing the last two results shows that the white area is half that of the regular polygon $A_0A_1\dots A_ {2m-2}A_ {2m-1}$; clearly, the total black area will be the same. This completes the proof of the lighter version of the pizza problem.

Discussion

1. The original pizza problem can be generalised to an arbitrary number of chords passing through the given point provided that: (i) the angle between any two consecutive ones is the same, and (ii) there is an even number of white and black slices. Following¹ we have discussed the case of $4$ chords which split the $360^\circ$ angle at $P$ into eight equal parts (so the angle between any two consecutive chords was $360^\circ/8 = 45^\circ$. For six chords this angle will be $360^\circ/12 = 30^\circ$, and so on.
2. The use of complex variables to re-interpret various results from analytic geometry is fairly old. The book by Mihaileanu³ contains a large number of classic plane geometry results re-worked in the language of complex numbers. Some of the references mentioned by him go back to the 1920-1930’s. An expanded version of that material can be found in a more recent student-friendly book by Andreescu and Andrica⁴. The text by Modenov⁵ is a classic problem book in geometry that uses extensively vectors and complex variables for some quite challenging scenarios. Perhaps the best treatment of complex numbers and geometry is an older text by Zwikker⁶, which blends high pedagogical values with a multitude of information; this is a very skillfully written book that benefits immensely from the careful typesetting by the publisher (a Dover edition was published later, but what I am referring to here is the initial hardcover edition). The book by Hahn⁷ also covers the standard fare from 2D geometry (the Simson line, the nine-point circle, Menelaus, etc), as well as some more esoteric stuff about the Mobius transformation; there are no references or bibliography included in this last one.
3. L.J. Upton⁸ initially introduced the pizza problem in 1967; its numerous generalisations have been extensively examined since then.

Footnotes

1. Konhauser, J.D.E., Velleman, D., Wagon, S.: Which Way Did the Bicyle Go?, The Mathematical Association of America (1997). ↩ ↩² ↩³ ↩⁴

2. Adams, R.: Calculus: A Complete Course. Addison Wesley, Boston (2003). ↩

3. Mihaileanu, N.: The Use of Complex Numbers in Geometry (in Romanian). Editura Technica, Bucharest (1968). ↩ ↩²

4. Andreescu, T.., Andrica, D.: Complex Numbers from A to… Z. Birkhausser, Boston (2005). ↩ ↩²

5. Modenov, P.S.: Problems in Geometry. Mir Moscow, URSS (1981). ↩

6. Zwikker, C.: Advanced Plane Geometry. North-Holland, Amsterdam (1950). ↩

7. Hahn, L-S.: Complex Numbers and Geometry, The Mathematical Association of America (1996). ↩

8. Upton, L.J.: Problem 660, Mathematics Magazine, Vol. 40, No. 3, p. 163 (1967). ↩