Curious numbers
The topic of this post is related to the following result.
Proposition 1
Consider six positive numbers $x_j$, $y_j$, $z_j$ ($j=1,2$) such that $0 < x_1 \le y_1 \le z_1$
and $x_1 \le x_2, y_2, z_2 \le z_1$. If
then { $x_1$, $y_1$, $z_1$ } $=$ { $x_2$, $y_2$, $z_2$ }. In other words, the two sets of numbers are equal to each other (in some order, which is irrelevant here).
Solution
Bringing everything over a common denominator in the second relation above gives
\[\dfrac{x_2y_2 + y_2z_2 + z_2x_2}{x_1y_1 + y_1z_1 + z_1x_1} = \dfrac{x_2y_2z_2}{x_1y_1z_1}\,. \tag{1}\]Letting $\lambda>0$ be the common value of the two fractions in (1), we can then write
\[x_2y_2 + y_2z_2 + z_2x_2 = \lambda(x_1y_1 + y_1z_1 + z_1x_1) \tag{2}\]and
\[x_2y_2z_2 = \lambda(x_2y_2z_2). \tag{3}\]Our goal is to show that $\lambda=1$ is the only choice compatible with the given hypotheses. To this end, we consider the third-order polynomial, $P$ (say), which has the numbers $x_2$, $y_2$, $z_2$ as its zeros; similarly, $Q$ will be the third-order polynomial with roots $x_1$, $y_1$, $z_1$
\[\begin{aligned}[t] &P(k) = k^3 - A_2k^2 + B_2k - C_2\\ &Q(k) = k^3 - A_1k^2 + B_1k - C_1. \end{aligned}\]According to Viete’s formulae,
\[A_2 = x_2+y_2+z_2,\qquad B_2 = x_2y_2 + y_2z_2 + z_2x_2,\qquad C_2 = x_2y_2z_2\]and a set of similar relations for the coefficients of $Q$. At this juncture we take advantage of (2) and (3) and notice that $A_1=A_2$, $B_2 = \lambda{B_1}$, and $C_2 = \lambda{C_1}$. Thus,
\[\begin{aligned}[t] &P(k) = k^3 - A_1k^2 + \lambda{B_1}k - \lambda{C_1}\\ &Q(k) = k^3 - A_1k^2 + B_1k - C_1. \end{aligned}\]The next step hinges on the particular ordering of the two sets of roots for $P$ and $Q$. Using a particular version of the intermediate value theorem (typically referred to as Weierstrass-Bolzano’s theorem), we obtain
\[Q(x_1)= 0 \ge P(x_1)\quad\mbox{and}\quad P(z_1) \ge 0 = Q(z_1)\,,\]which can be shown to be equivalent to
\[(B_1x_1 - C_1)(\lambda-1)\le 0\quad\mbox{and}\quad (B_1z_1 - C_1)(\lambda-1)\ge 0,\]respectively. Since the first factors on the left-hand side in these two inequalities are positive expressions, the only possible choice is $\lambda=1$. In this case the two polynomials are identical, so their roots will match each other in some (arbitrary) order. The proof is now complete.
The origin of this result is intimately connected to a scenario I encountered a fairly long time ago.
A geometry problem
In a triangle ABC, let $h_a$, $h_b$, $h_c$ be the altitudes from $A$, $B$, $C$; let $r$ be the radius of the incircle and $R$ the radius of the circumcircle of the given triangle. Then
\[h_a + h_b + h_c = 4R+r\quad\Longleftrightarrow\quad \Delta{ABC}\mbox{ is equilateral}. \tag{4}\]Of course, this is just a trigonometry problem in disguise. It does require knowledge of some standard formulae; for example,
\[r = 4R\sin\dfrac{A}{2}\sin\dfrac{B}{2}\sin\dfrac{C}{2}\]and
\[h_a = 2R\sin{B}\sin{C},\quad h_b = 2R\sin{C}\sin{A},\quad h_c = 2R\sin{A}\sin{B},\]where $A$, $B$, $C$ denote the angles of $\Delta{ABC}$. Once $r$ and $R$ have been eliminated from the equality in (4), the rest of the solution becomes a straightforward grind – I will not elaborate on this approach (maybe in a future post).
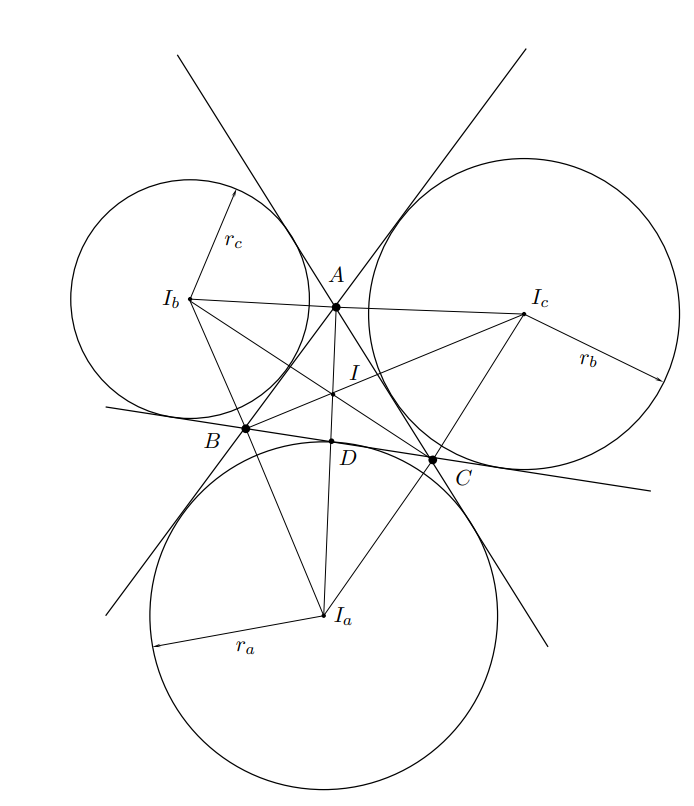
A more elegant solution can be given by using some less known identities for the radii of the excircles of $\Delta{ABC}$; these are denoted by $r_a$, $r_b$, $r_c$ (see sketch included below).
It is known that in any triangle
\[\dfrac{1}{r_a} + \dfrac{1}{r_b} + \dfrac{1}{r_c} = \dfrac{1}{r} =\dfrac{1}{h_a} + \dfrac{1}{h_b}+ \dfrac{1}{h_c} \tag{5}\]and
\[r_a + r_b + r_c = 4R+r. \tag{6}\]Taken in conjunction with the equality in (4), it is clear that the sets { $h_a$, $h_b$, $h_c$ } and { $r_a$, $r_b$, $r_c$ } satisfy the two equalities in Proposition 1, but we still need to check that the ordering relationships mentioned there are also fulfilled.
Assuming (without loss of generality) that $a\le {b}\le {c}$, it can be checked that
\[r_a\le r_b \le r_c,\quad h_a\ge h_b\ge h_c,\]and
\[r_a\le h_a, h_b, h_c\leq r_c.\]Finally, a close examination of all possible cases for the equality of the two sets of numbers shows that $a=b=c$ (i.e., the given triangle is an equilateral one).
Notes
Here is some additional information concerning the excircles:
- the angle bisector of $\angle{BAC}$ is the locus of points equidistant to the two lines $AB$ and $AC$. The angle just mentioned has in fact two bisectors, one internal and one external (the same is true for the other angles of $\Delta{ABC}$);
- the point $D$ in the above sketch represents the intersection between the internal bisector of $\angle{BAC}$ and the side $BC$;
- the internal bisectors of the three angles of the given triangle meet at a point that is equidistant to any side; this represents the centre of a circle tangent to all three sides of $\Delta{ABC}$, which is known as the inscribed circle or incircle;
- the internal bisector of $\angle{BAC}$ concurs with the external bisectors of the other two angles; the point of concurrence is the excentre opposite to $A$ – this is $I_a$ in the above sketch; $BI_a$ and $CI_a$ correspond to the external bisectors of $\angle{ABC}$ and $\angle{ACB}$, respectively;
- there exists a circle centred there (i.e., at $I_a$) that is tangent to all three sides – this is the excircle opposite to $A$; its radius is denoted by $r_a$; similarly, one can define the excircles opposite to $B$ and $C$, whose radii are denoted by $r_b$ and $r_c$, respectively;
- $r_a = \dfrac{S}{p-a}$, where $S=\sqrt{p(p-a)(p-b)(p-c)}$ is the area of the triangle and $p=(a+b+c)/2$ represents its semi-perimeter; $r_b$ and $r_c$ have similar expressions.