Victorious vectors
Intro
As the title suggests, this post is about vectors.
More than two millennia ago, the ancient Greeks asked a simple question: given three positive numbers a, b, and c, under what conditions can one construct a triangle whose sides have lengths equal to the three given numbers (in some arbitrary order) ? It turns out that such a triangle can be constructed provided that the following three simultaneous inequalities are satisfied:
\[a < b+c,\qquad b < a+c,\qquad c < a+b.\]The triangle inequality is usually a generic name given to each of these three inequalities.
Now, let’s consider the (geometrical) addition of vectors. This can be accomplished in two different ways. One of them is known as the triangle law and goes like this. Assume that we want to add two free vectors $\bf{u}$ and $\bf{v}$. To this end, we choose a point $A$ and construct the vector $\overrightarrow{AC}$ which has the same magnitude and direction as $\bf{u}$; using $C$ as the starting point, we also construct a vector $\overrightarrow{CB}$ such that it has the same magnitude and direction as $\bf{v}$. We then simply join $A$ and $B$; the vector $\overrightarrow{AB}$ corresponds to the (vector) sum of the originally given vectors $\bf{u}$ and $\bf{v}$. In terms of the sketch included below
\[\overrightarrow{AB}=\overrightarrow{AC}+\overrightarrow{CB}. \tag{1}\]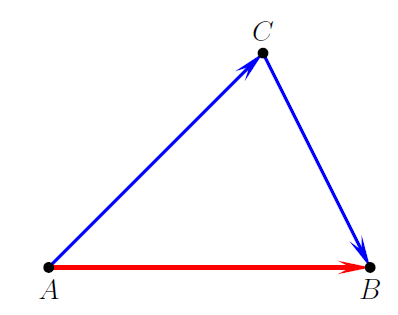
Obviously, in terms of distances (remembering the triangle inequality),
\[AB < AC + CB. \tag{2}\]This may seem to contradict (1). The key thing here to notice is that the last two formulae involve different mathematical objects. In (1) we have vectors, i.e. quantities that possess both magnitude and direction, while (2) involves just numbers. In fact, (1) is a result that we adopt as a definition for the addition of vectors (i.e., we can’t prove the triangle law for vector addition because it is essentially something that is postulated a priori).
As a side note, it is worth mentioning that the triangle inequality (2) can also be stated in a different way,
\[|\overrightarrow{AC}+\overrightarrow{CB}|<|\overrightarrow{AC}|+|\overrightarrow{CB}|\]or
\[|{\bf{u}} +{\bf{v}}|<|{\bf{u}}|+|{\bf{v}}|,\]where the vertical bars stand for the magnitude of the vectors they enclose.
(In writing the strict inequality sign we have assumed that $C$ is not situated on the line $AB$.)
Position vectors
Vectors come in quite handy when one has to keep track of the position of points (either in 2D or 3D). In general, this requires choosing a point $O$ (fixed, but arbitrary otherwise). The position vector of a point $P$ relative to $O$ is by definition the vector $\overrightarrow{OP}$; this vector uniquely identifies the position of $P$.
For any two points $A$ and $B$, the triangle law guarantees that the vector $\overrightarrow{AB}$ is equal to the difference between the position vectors of its endpoints (taken in reverse order), i.e.
\[\overrightarrow{AB} = \overrightarrow{OB}-\overrightarrow{OA} = p.v.(B) - p.v.(A)\]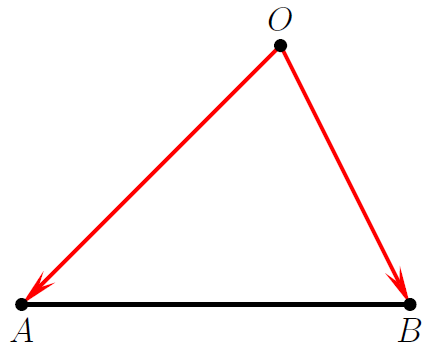
A common situation in geometry involves an arbitrary point situated on a line, which is determined by two other (fixed) points whose position vectors (relative to some origin) are known. It turns out that the position vector of the aforementioned arbitrary point can be found very easily, as explained next.
If $P$ is a point on a line $AB$, then the vectors $\overrightarrow{AP}$ and $\overrightarrow{PB}$ are parallel, so that
\[\overrightarrow{AP} = \lambda\overrightarrow{PB}, \tag{3}\]for some scalar $\lambda\in\mathbb{R}$. We call $\lambda$ the position ratio of $P$ with respect to $A$ and $B$, and often write
\[\dfrac{AP}{PB} = \lambda. \tag{4}\]It is important to realise (4) is just a convenient way of writing (3). In the former representation we are not quite talking about the ratio of the distance $AP$ to the distance $PB$. We are actually talking of the ratio of the signed distances $AP$ and $PB$, where we regard a distance as positive if it is measured in the direction from $A$ to $B$, and negative if it is measured in the opposite direction.
We come now to the main result:
The Section Formula (SF)
Let $P$ be any point on the line $AB$ with position ratio
\[\dfrac{AP}{PB} = \dfrac{m}{n}\qquad \mbox{(as defined above)}.\]Then $\overrightarrow{OP}$, the position vector of $P$, is given by
\[\overrightarrow{OP} = \dfrac{n\overrightarrow{OA}+m\overrightarrow{OB}}{m+n}\]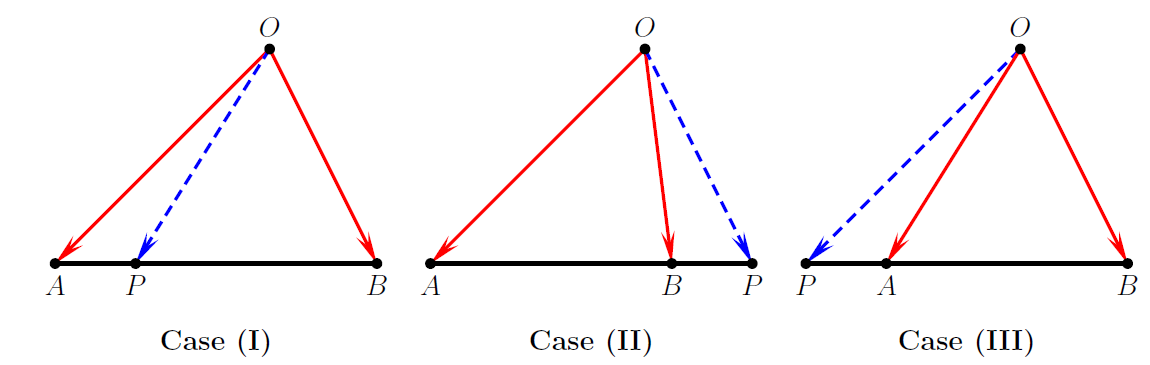
The SF is still valid when either $m$ or $n$ is negative. In Case (I) in the above sketch, the position ratio of $P$ relative to $A$ and $B$ is positive (in this case $m$, $n>0$), whereas in Cases (II) and (III) this position ratio is negative (since one of the numbers $m$ and $n$ must be negative).
We will now look at a non-trivial example in which the SF proves to be quite useful.
Example
The vertices $A$, $B$, $C$ of a triangle $ABC$ have position vectors $\bf{a}$, $\bf{b}$, $\bf{c}$, respectively. $D$, $E$, $F$ are points on the lines $AC$, $AB$, $BC$, respectively, such that $AD/DC=1/2$, $AE/EB=3/2$, $BF/FC=-1/3$. Express the position vectors of $D$, $E$, $F$ in terms of $\bf{a}$, $\bf{b}$, $\bf{c}$. Hence prove that $D$, $E$, $F$ are collinear and find the value of $DE/EF$.
Before we start, I should say that one can prove the collinearity of the three points mentioned above quite easily by using a classic theorem attributed to Menelaus of Alexandria.
Let’s start the (SF-based) solution by first introducing some notation:
\[{\bf{d}}\equiv p.v.(D),\qquad {\bf{e}}\equiv p.v.(E),\qquad {\bf{f}}\equiv p.v.(F).\]Using the position ratios mentioned in the problem, the use of the SF yields
\[{\bf{d}} = \dfrac{1}{3}(2{\bf{a}} + {\bf{c}})\,\qquad {\bf{e}} = \dfrac{1}{5}(2{\bf{a}} + 3{\bf{b}})\,\qquad {\bf{f}} = \dfrac{1}{2}(3{\bf{b}} - {\bf{c}}).\]It is worth taking a closer look at the last relation in these formulae. Note the following
\[\dfrac{BF}{FC}=-\dfrac{1}{3}=\dfrac{-1}{3}\equiv\dfrac{m}{n}\qquad\Longrightarrow\qquad m=-1\quad\mbox{and}\quad n=3.\] \[{\bf{f}}\equiv \overrightarrow{OF} = \dfrac{n\overrightarrow{OB}+m\overrightarrow{C}}{m+n} = \dfrac{(3){\bf{b}}+(-1){\bf{c}}}{3+(-1)} = \dfrac{1}{2}(3{\bf{b}} - {\bf{c}}),\]where $O$ is a fixed origin (as explained above). The same result follows if we take $m=1$ and $n=-3$.
Since we have the position vectors of $D$, $E$, $F$ in terms of those of the vertices of the original triangle, we would expect the vectors $\overrightarrow{DE}$ and $\overrightarrow{EF}$ to enjoy the same property. Indeed,
\[\begin{aligned}[t] \overrightarrow{DE} = {\bf{e}}-{\bf{d}} &= \dfrac{1}{5}(2{\bf{a}}+3{\bf{b}}) - \dfrac{1}{3}(2{\bf{a}}+{\bf{c}})\\ &=\dfrac{1}{15}(-4{\bf{a}}+9{\bf{b}}-5{\bf{c}}) \end{aligned} \tag{5}\]and
\[\begin{aligned}[t] \overrightarrow{EF} = {\bf{f}}-{\bf{e}} &= \dfrac{1}{2}(3{\bf{b}}-{\bf{c}}) - \dfrac{1}{5}(2{\bf{a}}+3{\bf{b}})\\ &=\dfrac{1}{10}(-4{\bf{a}}+9{\bf{b}}-5{\bf{c}}) \end{aligned} \tag{6}\]Comparing (5) and (6) we find that
\[\overrightarrow{DE} = \dfrac{2}{3}\overrightarrow{EF},\]i.e. these two vectors are scalar multiples of each other; since they also have a point in common it follows that $D$, $E$, $F$ are collinear, as required. Noting further that the direction from $D$ to $E$ is the same as that from $E$ to $F$, we finally conclude that $DE/EF = 2/3$. This completes the solution of our example.
Additional notes
If you would like to practise more questions similar to this example, you can follow this link (weeks 2 and 3).